第7回講義資料

変数間の関係

スライド

新しいタブで開く

セットアップ

　今回の実習で使用するパッケージとデータセットを読み込む。各データセットの詳細はスライドを参照すること。

Code 01

library(tidyverse)
library(summarytools)
library(fastDummies)

gacha_df   <- read_csv("Data/Gacha2.csv")
subsidy_df <- read_csv("Data/Subsidy.csv")
pasta_df   <- read_csv("Data/Pasta.csv")

\(t\)検定

　まずはgacha_dfの中身を確認する。このデータは前回講義データと同じデータであるが、ガチャ結果（result）の列をダミー変数にしたものを追加したデータである。

Code 02

gacha_df

# A tibble: 4,772 × 8
   player trial stone_type result result_N result_R result_SR result_SSR
    <dbl> <dbl> <chr>      <chr>     <dbl>    <dbl>     <dbl>      <dbl>
 1      1     1 Paid       R             0        1         0          0
 2      1     2 Paid       R             0        1         0          0
 3      1     3 Paid       SR            0        0         1          0
 4      1     4 Free       R             0        1         0          0
 5      1     5 Paid       N             1        0         0          0
 6      1     6 Free       N             1        0         0          0
 7      1     7 Free       SSR           0        0         0          1
 8      1     8 Free       N             1        0         0          0
 9      1     9 Free       N             1        0         0          0
10      1    10 Free       N             1        0         0          0
# ℹ 4,762 more rows

　続いて、{summarytools}のdescr()関数でgacha_dfの記述統計を確認する。出力する記述統計量は平均値、標準偏差、最小値、最大値、有効ケース数である。また、プレイヤーのID（layer）はデータ上は数値型ではあるものの、実質名目変数であるため、記述統計から除外する。

Code 03

gacha_df |>
  select(-player) |> # player列を除外してdescr()関数に渡す
  descr(stats = c("mean", "sd", "min", "max", "n.valid"),
        transpose = TRUE, order = "p")

Descriptive Statistics  

                    Mean   Std.Dev    Min     Max   N.Valid
---------------- ------- --------- ------ ------- ---------
           trial   34.01     24.22   1.00   99.00   4772.00
        result_N    0.56      0.50   0.00    1.00   4772.00
        result_R    0.25      0.43   0.00    1.00   4772.00
       result_SR    0.15      0.35   0.00    1.00   4772.00
      result_SSR    0.05      0.21   0.00    1.00   4772.00

　問題は石の種類（stone_type）とガチャの結果（result）が文字型変数であることから記述統計量が表示されない点である。ガチャの結果は既にダミー変数（result_で始まる4つの変数）になっているので問題ないが、石の種類はもう一度ダミー変数に変換する必要がある。

　今回はダミー化した石の種類を分析に使う予定はなく、記述統計量さえ見られるのであれば十分だ。したがって、gacha_dfをdescr()関数に渡す前にdummy_cols()関数でダミー変数化する。

Code 04

gacha_df |>
  # ダミー化する変数が複数の場合、
  # select_columns = c("変数名1", "変数名2", "変数名3")
  # と書く
  dummy_cols(select_columns = "stone_type", ignore_na = TRUE) |>
  select(-c(player, stone_type, result)) |>
  descr(stats = c("mean", "sd", "min", "max", "n.valid"),
        transpose = TRUE, order = "p")

Descriptive Statistics  

                         Mean   Std.Dev    Min     Max   N.Valid
--------------------- ------- --------- ------ ------- ---------
                trial   34.01     24.22   1.00   99.00   4772.00
             result_N    0.56      0.50   0.00    1.00   4772.00
             result_R    0.25      0.43   0.00    1.00   4772.00
            result_SR    0.15      0.35   0.00    1.00   4772.00
           result_SSR    0.05      0.21   0.00    1.00   4772.00
      stone_type_Free    0.66      0.48   0.00    1.00   4772.00
      stone_type_Paid    0.34      0.48   0.00    1.00   4772.00

　検定の前にgroup_by()関数とsummarise()関数を使用し、石の種類（stone_type）ごとのSSR出現有無（result_SSR）の平均値を計算してみよう。結果はmean_dfという名のオブジェクトとして格納する。

Code 05

mean_df <- gacha_df |>
  group_by(stone_type) |>
  summarise(SSR = mean(result_SSR, na.rm = TRUE))

mean_df

# A tibble: 2 × 2
  stone_type    SSR
  <chr>       <dbl>
1 Free       0.0425
2 Paid       0.0572

　2つの出現割合の差は0.0425 - 0.0572、約-0.015であり、これを%で換算すると約-1.5%ポイントである。つまり、無償石の方が有償石に比べSSR出現の割合が約1.5%ポイント低いことを意味する。これを棒グラフで示すと以下のようになる。

Code 06

mean_df |>
  ggplot() +
  # geom_col()の代わりに、以下のgeom_bar()でもOK
  # geom_bar(aes(x = stone_type, y = SSR), stat = "identity") +
  geom_col(aes(x = stone_type, y = SSR)) +
  labs(x = "石の種類", y = "SSRの出現割合")

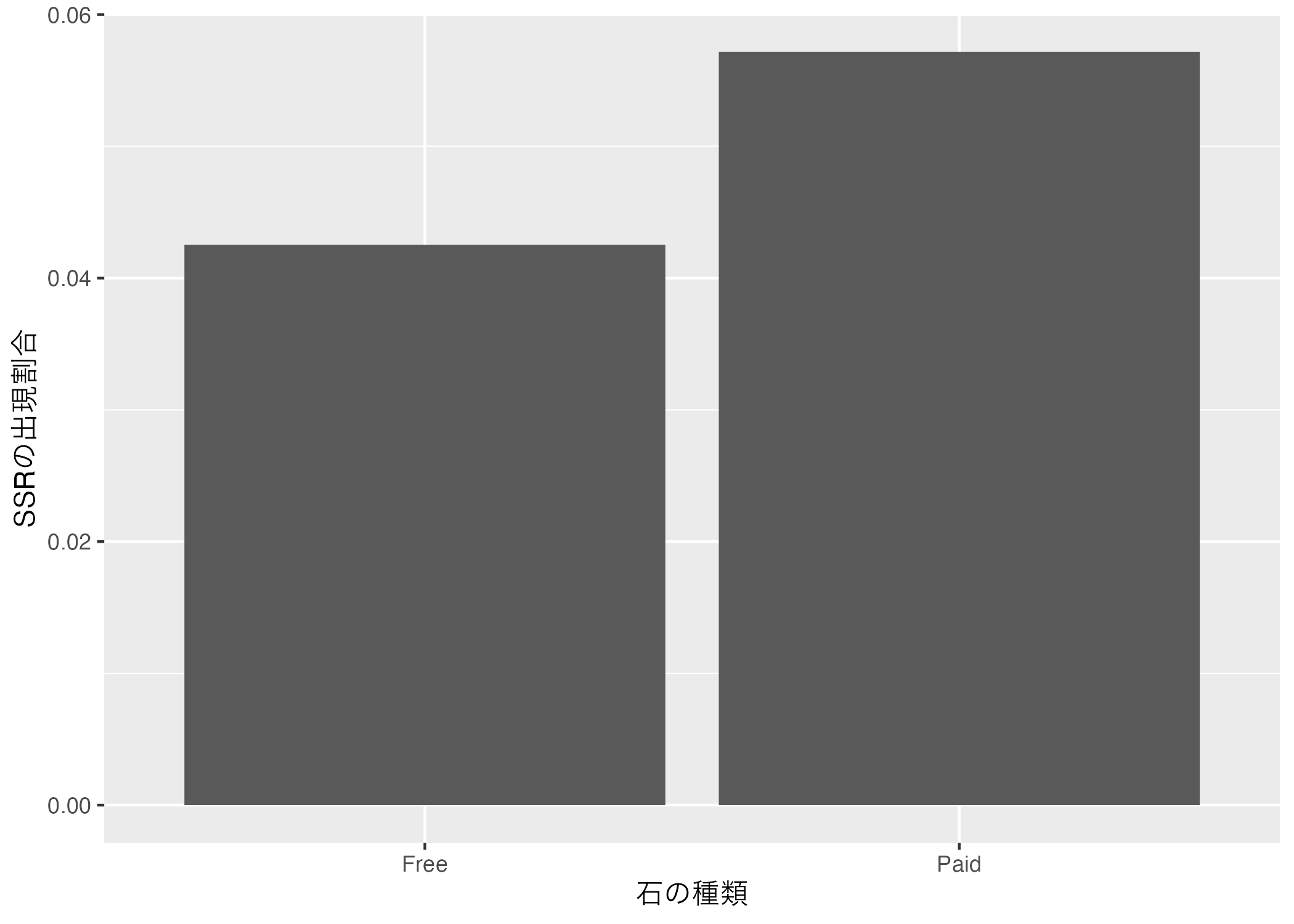
　図に英語と日本語が混在することは良くないので、mean_dfをggplot()に渡す前にstone_typeを日本語にリコーディングし、SSR列には100をかけて%に換算する。リコーディングは3値以上であれば、case_when()、またはrecode()を使うが、今回は"Free"か"Paid"かの2値となるので、if_else()を使用する。

# if_else()の使い方
if_else(条件式, 条件がTRUEの場合の戻り値, 条件がFALSEの場合の戻り値)

　今回はstone_typeが"Feee"であれば（stone_type == "Free"）、"無償"と、それ以外は"有償"とリコーディングする。

Code 07

mean_df |>
  mutate(stone_type = if_else(stone_type == "Free", "無償", "有償"),
         SSR        = SSR * 100) |>
  ggplot() +
  geom_col(aes(x = stone_type, y = SSR)) +
  labs(x = "石の種類", y = "SSRの出現割合 (%)") +
  # テーマをblack and whiteにし、文字サイズを14に
  theme_bw(base_size = 14)

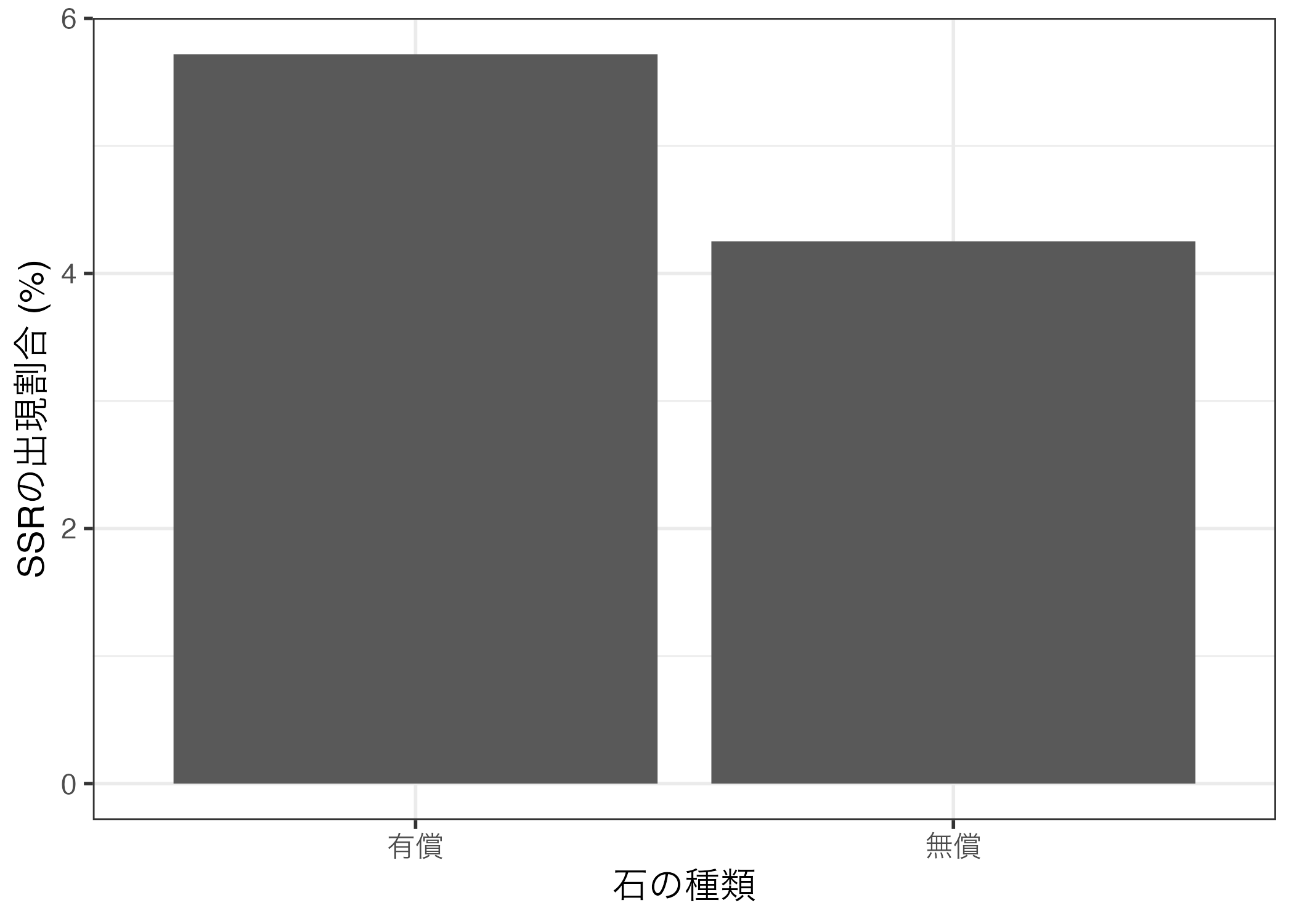
　最後にこの約-1.5%ポイントの差が統計的に有意な差かどうかを検定してみよう。検定の際、帰無仮説は「無償石のSSRの確率と有償石のSSRの確率の差は0である」であり、対立仮説は「無償石のSSRの確率と有償石のSSRの確率の差は0ではない」となる。有意水準（\(\alpha\)）は予め0.05と設定しておく。

　（2群の）平均値の差の検定にはt.test()を利用する。第一引数は回帰式であり、書き方は「平均値の差を見る変数名 ~ グループを示す変数名」である。今回は石の種類（stone_type）ごとのSSR出現有無（result_SSR）の平均値の差を検定するため、result_SSR ~ stone_typeと指定する。第二引数はdataであり、これらの変数が格納されているデータのオブジェクト名（今回はgacha_df）を指定する。

Code 08

t.test(result_SSR ~ stone_type, data = gacha_df)

    Welch Two Sample t-test

data:  result_SSR by stone_type
t = -2.1653, df = 2960.6, p-value = 0.03045
alternative hypothesis: true difference in means between group Free and group Paid is not equal to 0
95 percent confidence interval:
 -0.027932426 -0.001384442
sample estimates:
mean in group Free mean in group Paid 
        0.04251918         0.05717762 

　今回の例の場合、「SSRの出現有無」が0か1のダミー変数であるため、厳密な意味では平均値の差の検定（\(t\)検定）よりも比率の差の検定が適切である。実は平均値の差の検定と比率の差の検定の結果が大きくずれることはほぼないが（点推定値は必ず一致する）、念の為にprop.test()を利用して比率の差の検定を行ってみよう。

　prop.test()にはxとnの2つの引数が必要であり、それぞれ成功の回数と試行回数のベクトルを指定する。今回は無償石で133回、有償石で94回SSRが引けたため、x = c(133, 94)を指定する。また、無償石でのガチャ回数は3128回、有償石のそれは1664回だったのでn = c(3128, 1644)と指定する。

Code 09

prop.test(x = c(133, 94), n = c(3128, 1644))

    2-sample test for equality of proportions with continuity correction

data:  c(133, 94) out of c(3128, 1644)
X-squared = 4.7923, df = 1, p-value = 0.02859
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.0283874901 -0.0009293778
sample estimates:
    prop 1     prop 2 
0.04251918 0.05717762 

　平均値の差の検定と比率の差の検定の結果において点推定値は必ず一致するが、\(p\)値や信頼区間にやや違いが生じる。今回の\(p\)値は約0.029である。\(t\)検定では約0.030であったため、その違いは約0.001であり、帰無仮説が棄却できる点では同じ結果が得られた。

両手法の比較

手法	点推定値	\(p\)値	95%信頼区間（下限）	95%信頼区間（上限）
平均値の差の検定	-0.015	0.030	-0.028	-0.001
比率の差の検定	-0.015	0.029	-0.028	-0.001

\(t\)検定は2群間の平均値の差の検定

　もし平均値を比較するグループが3つ以上である場合は、\(t\)検定を行わず、分散分析（Analysis of variance; ANOVA）を実施する。詳しいことはインターネットで検索してみよう。

相関分析

　まずはsubsidy_dfの中身を確認してみよう。

Code 10

subsidy_df

# A tibble: 47 × 4
      ID Pref   Turnout Subsidy
   <dbl> <chr>    <dbl>   <dbl>
 1     1 北海道    60.3   134. 
 2     2 青森県    54.2   193. 
 3     3 岩手県    59.1   265. 
 4     4 宮城県    52.8    98.2
 5     5 秋田県    60.6   219. 
 6     6 山形県    64.1   187. 
 7     7 福島県    56.7   166. 
 8     8 茨城県    51.5    76.3
 9     9 栃木県    51.7    72.8
10    10 群馬県    52.0    76.6
# ℹ 37 more rows

　つづいて、当該都道府県の投票率（Turnout）と一人あたり補助金額（Subsidy）の記述統計量を確認する。

Code 11

subsidy_df |>
  select(Turnout, Subsidy) |>
  descr(stats = c("mean", "sd", "min", "max", "n.valid"),
        transpose = TRUE, order = "p")

Descriptive Statistics  

                  Mean   Std.Dev     Min      Max   N.Valid
------------- -------- --------- ------- -------- ---------
      Turnout    54.91      4.01   46.47    64.07     47.00
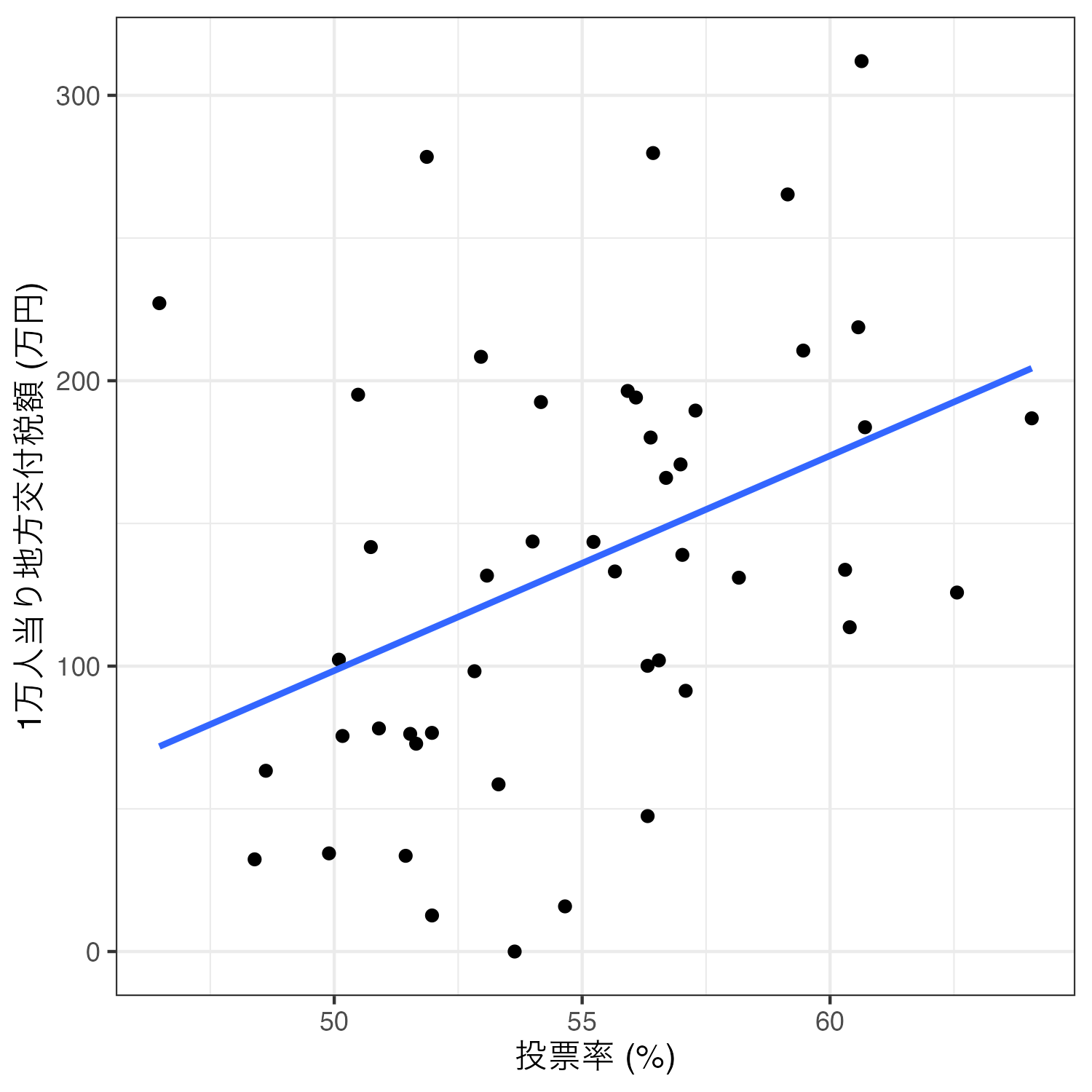
      Subsidy   135.40     75.88    0.00   311.98     47.00

　相関分析を行う場合、主に（１）散布図の作成と（２）相関係数の計算（と統計的有意性検定）が必要となる。まずは、散布図を作成してみよう。今回は横軸が投票率、縦軸が一人あたり補助金額の散布図を作成する。

Code 12

# subsidy_dfを使って
subsidy_df |>
  # キャンバスを用意する
  ggplot() +
  # 横軸（x）が投票率（Turnout）、縦軸（y）が補助金額（Subsidy）の
  # 散布図（geom_point()）を作成する。
  geom_point(aes(x = Turnout, y = Subsidy)) +
  # 横軸と縦軸のラベルを修正する。
  labs(x = "投票率 (%)", y = "1万人当り地方交付税額 (万円)") +
  # 白黒テーマを使用する。
  theme_bw()

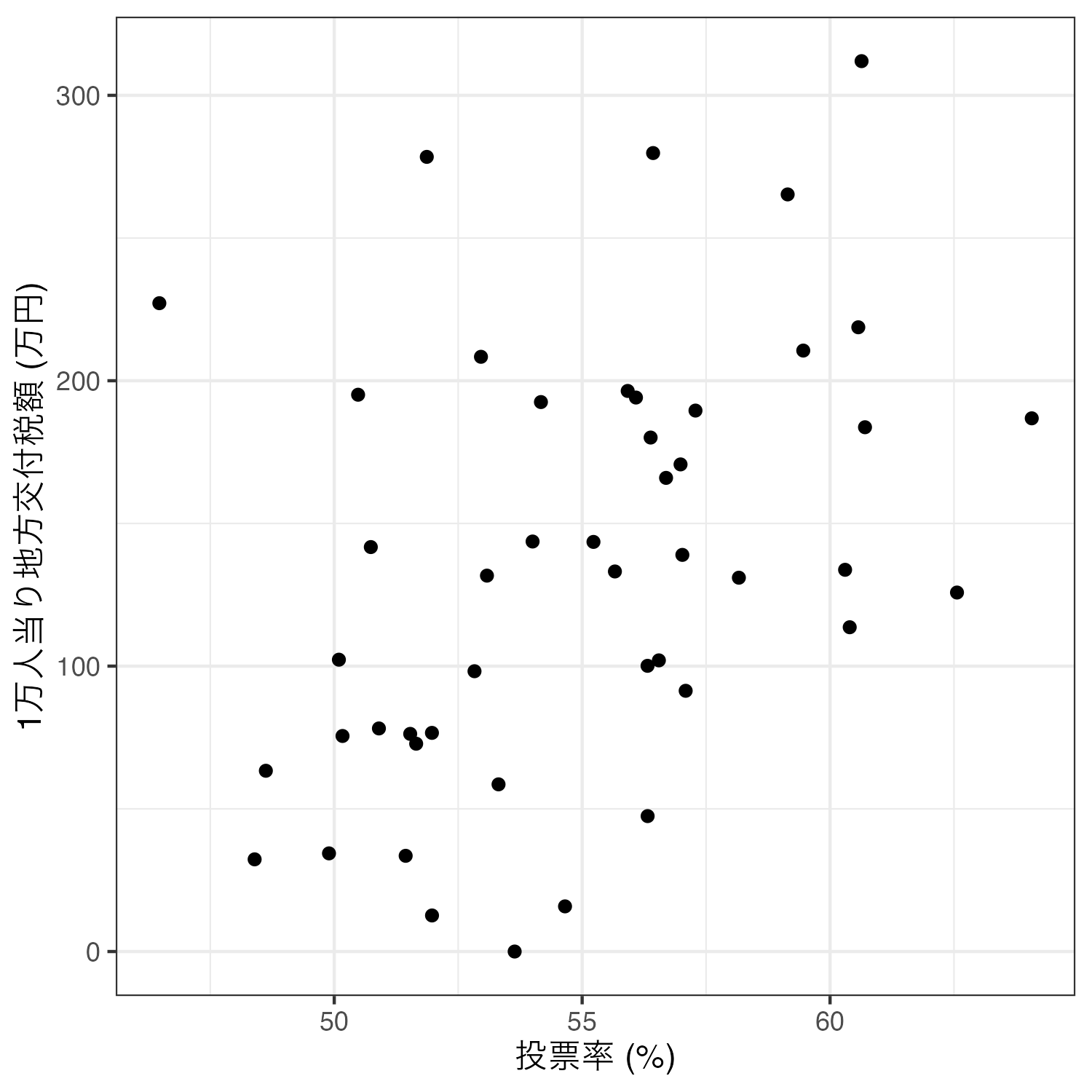
　2つの変数の関係を最も適切に表す直線（=回帰直線）を追加するためには、geom_smooth()レイヤーを足す。2次元平面上の散布図の場合、xとyは同じ変数をマッピングする必要がある。また、直線を出すためにはmethod = "lm"引数を追加し、95%信頼区間を消すためにse = FALSEも追加する。余裕があれば、各引数を消した場合の結果も確認してみよう。

Code 13

subsidy_df |>
  ggplot() +
  geom_point(aes(x = Turnout, y = Subsidy)) +
  # 2つの変数間の関係を示す直線（回帰直線; method = "lm"）を引く
  # 信頼区間は表示しない（se = FALSE）
  geom_smooth(aes(x = Turnout, y = Subsidy), 
              method = "lm", se = FALSE) +
  labs(x = "投票率 (%)",
       y = "1万人当り地方交付税額 (万円)") +
  theme_bw()

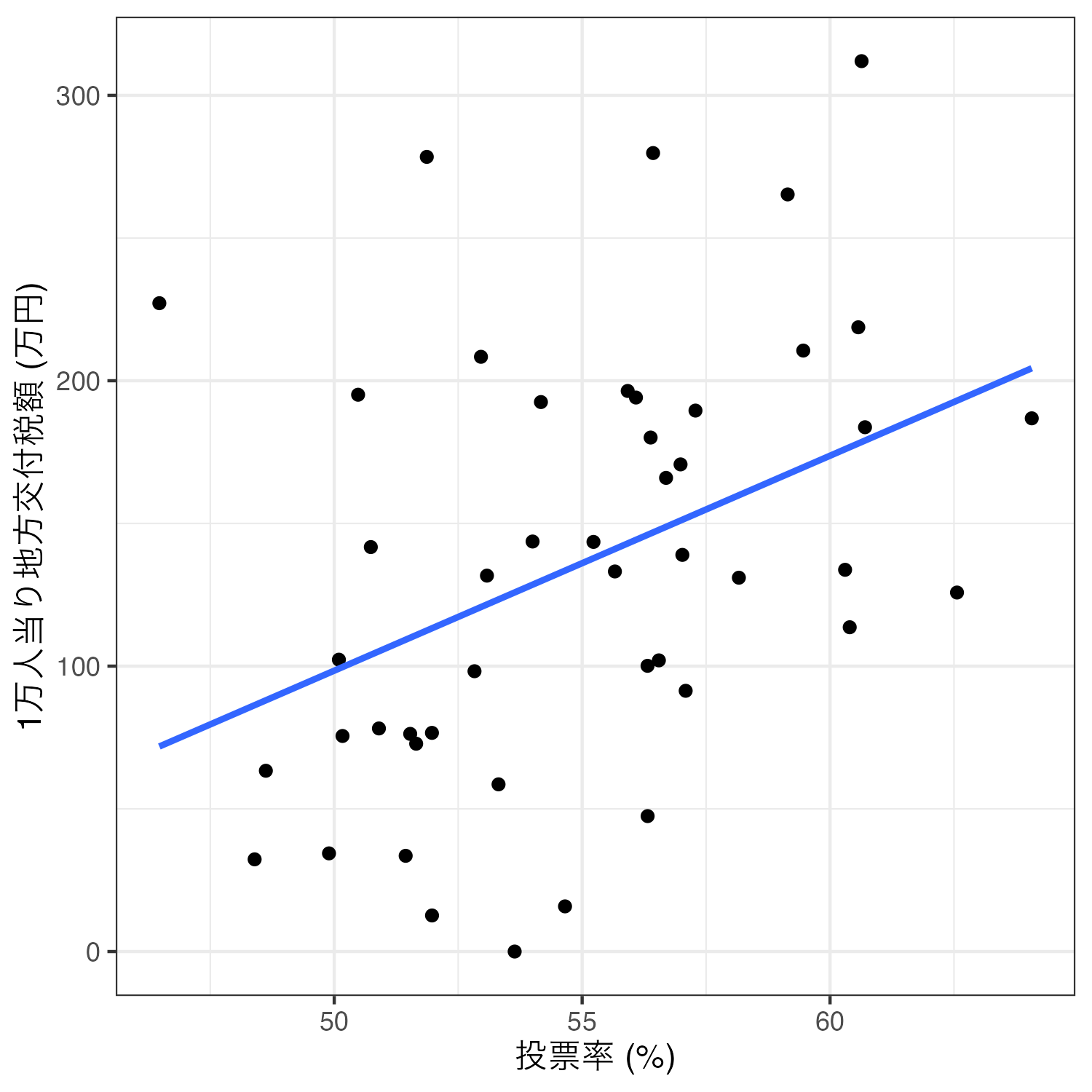
　これで散布図+回帰直線の図は完成したが、より効率的なコードの書き方がある。先ほどのコードの場合、geom_point()とgeom_smooth()のマッピング（aes()関数の内部）は共通する要素があり、それはx = Turnoutとy = Subsidyである。複数の幾何オブジェクト（geom_で始まる関数）がマッピングを共有する場合は、以下のようにggplot()内部でマッピングを指定することができる。

Code 14

subsidy_df |>
  # 2つの幾何オブジェクト（geom_関数）はマッピング（xとy）を共有するため
  # ggplot()内で定義した方が効率的
  ggplot(aes(x = Turnout, y = Subsidy)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  labs(x = "投票率 (%)",
       y = "1万人当り地方交付税額 (万円)") +
  theme_bw()

　最後に相関係数を計算し、統計的有意性検定を行ってみよう。Rが提供する相関分析の関数はいくつかあるが、統計的有意性検定も同時に行う場合はcor.test()を使用する。引数は相関係数を計算する2つのベクトルを指定する。今回はsubsidy_dfのTurnout列（subsidy_df$Turnout）とsubsidy_dfのSubsidy列（subsidy_df$Subsidy）がそれである。

順序変数の場合は?

　今回の例は「連続変数\(\times\)連続変数」の相関分析であるが、「順序変数\(\times\)順序変数」もしくは「順序変数\(\times\)連続変数」の相関分析も可能である。しかし、cor.test()に第3引数としてmethod = "spearman"、またはmethod = "kendall"を追加すること。

Code 15

# with(subsidy_df, cor.test(Turnout, Subsidy)) もOK
cor.test(subsidy_df$Turnout, subsidy_df$Subsidy)

    Pearson's product-moment correlation

data:  subsidy_df$Turnout and subsidy_df$Subsidy
t = 2.9128, df = 45, p-value = 0.005558
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.1254750 0.6151042
sample estimates:
      cor 
0.3982905 

　相関係数は約0.398であり、\(p\)値は約0.006である。\(p\)値が一般的に使われる有意水準（\(\alpha = 0.05\)）より小さいことから、統計的に有意な「正の」相関関係があると考えられる。つまり、「投票率が高い都道府県ほど一人あたり補助金額が多い傾向がある」ことを意味する。

　ただし、この相関関係が因果関係、つまり「投票率が上がると補助金額が増える」ということを意味するわけではない。そもそも投票率が原因で、補助金額が結果であるかどうかすらも不明である。補助金額が増えることによって、有権者がその見返りとして投票に参加したかも知れない。相関関係と因果関係は厳格に区別すべきであり、そのためには緻密な理論・仮説、もしくは研究デザインが必要である。

\(\chi^2\)検定

　まずはpasta_dfの中身を確認してみよう。

Code 16

pasta_df

# A tibble: 1,135 × 4
      ID Female Over40 Pasta      
   <dbl>  <dbl>  <dbl> <chr>      
 1     1      0      0 Naporitan  
 2     2      1      0 Naporitan  
 3     3      0      0 Naporitan  
 4     4      0      0 Carbonara  
 5     5      0      0 Naporitan  
 6     6      0      1 MeatSauce  
 7     7      0      1 Peperoncino
 8     8      0      1 MeatSauce  
 9     9      1      0 Carbonara  
10    10      0      0 Carbonara  
# ℹ 1,125 more rows

　つづいて、Female変数とOver40変数をリコーディングし、それぞれGender_DとOver40_Dという新しい列として追加する。具体的にはFemaleの値が1なら"Female"、それ以外は"Male"の値を割り当てたGender_D変数を作成し、Over40の値が1なら"41 to 80"、それ以外は"18 to 40"の値を割り当てたOver40_Dを作成する。各変数はfactor()関数を使ってfactor化する。要素の順番はGender_Dの場合"Male"、"Female"、Over40_Dは"18 to 40"、"41 to 80"とする。

Code 17

pasta_df <- pasta_df |>
  mutate(Gender_D = if_else(Female == 1, "Female", "Male"),
         Gender_D = factor(Gender_D, levels = c("Male", "Female")),
         Over40_D = if_else(Over40 == 1, "41 to 80", "18 to 40"),
         Over40_D = factor(Over40_D, levels = c("18 to 40", "41 to 80")))

pasta_df

# A tibble: 1,135 × 6
      ID Female Over40 Pasta       Gender_D Over40_D
   <dbl>  <dbl>  <dbl> <chr>       <fct>    <fct>   
 1     1      0      0 Naporitan   Male     18 to 40
 2     2      1      0 Naporitan   Female   18 to 40
 3     3      0      0 Naporitan   Male     18 to 40
 4     4      0      0 Carbonara   Male     18 to 40
 5     5      0      0 Naporitan   Male     18 to 40
 6     6      0      1 MeatSauce   Male     41 to 80
 7     7      0      1 Peperoncino Male     41 to 80
 8     8      0      1 MeatSauce   Male     41 to 80
 9     9      1      0 Carbonara   Female   18 to 40
10    10      0      0 Carbonara   Male     18 to 40
# ℹ 1,125 more rows

　独立性の検定を行う前に、2つの名目変数のクロス表から作成する。ここでは2つのクロス表を作成する。1つ目は性別（Gender_D）と好きなパスタ（Pasta）のクロス表、2つ目はj年齢（Over40_D）と好きなパスタ（Pasta）のクロス表である。作り方はtable()関数の中に2つの名目変数のベクトルを指定するだけだ。

Code 18

# with(pasta_df, table(Female, Pasta)) もOK
table(pasta_df$Gender_D, pasta_df$Pasta)

        
         Carbonara MeatSauce Naporitan Peperoncino
  Male         139       201       145         105
  Female       139       160       153          93

# with(pasta_df, table(Over40, Pasta)) もOK
table(pasta_df$Over40_D, pasta_df$Pasta)

          
           Carbonara MeatSauce Naporitan Peperoncino
  18 to 40       138       177       160          65
  41 to 80       140       184       138         133

　周辺分布を追加するためには、クロス表をパイプ演算子を使ってaddmargins()関数に渡せば良い。

Code 19

table(pasta_df$Gender_D, pasta_df$Pasta) |>
  addmargins()

        
         Carbonara MeatSauce Naporitan Peperoncino  Sum
  Male         139       201       145         105  590
  Female       139       160       153          93  545
  Sum          278       361       298         198 1135

table(pasta_df$Over40_D, pasta_df$Pasta) |>
  addmargins()

          
           Carbonara MeatSauce Naporitan Peperoncino  Sum
  18 to 40       138       177       160          65  540
  41 to 80       140       184       138         133  595
  Sum            278       361       298         198 1135

　また、クロス表を度数（frequency）でなく、割合で示すこともできる。この場合、クロス表をprop.table()関数に渡すだけで良い。

Code 20

table(pasta_df$Gender_D, pasta_df$Pasta) |>
  prop.table()

        
          Carbonara  MeatSauce  Naporitan Peperoncino
  Male   0.12246696 0.17709251 0.12775330  0.09251101
  Female 0.12246696 0.14096916 0.13480176  0.08193833

table(pasta_df$Over40_D, pasta_df$Pasta) |>
  prop.table()

          
            Carbonara  MeatSauce  Naporitan Peperoncino
  18 to 40 0.12158590 0.15594714 0.14096916  0.05726872
  41 to 80 0.12334802 0.16211454 0.12158590  0.11718062

　むろん、割合のクロス表を更にaddmargins()に渡すことで、周辺分布を追加することもできる。

Code 21

table(pasta_df$Gender_D, pasta_df$Pasta) |>
  prop.table() |>
  addmargins()

        
          Carbonara  MeatSauce  Naporitan Peperoncino        Sum
  Male   0.12246696 0.17709251 0.12775330  0.09251101 0.51982379
  Female 0.12246696 0.14096916 0.13480176  0.08193833 0.48017621
  Sum    0.24493392 0.31806167 0.26255507  0.17444934 1.00000000

table(pasta_df$Over40_D, pasta_df$Pasta) |>
  prop.table() |>
  addmargins()

          
            Carbonara  MeatSauce  Naporitan Peperoncino        Sum
  18 to 40 0.12158590 0.15594714 0.14096916  0.05726872 0.47577093
  41 to 80 0.12334802 0.16211454 0.12158590  0.11718062 0.52422907
  Sum      0.24493392 0.31806167 0.26255507  0.17444934 1.00000000

　また、割合を0〜1でなく、0%〜100%で表示したい場合は、更に100をかければ良い。数学・統計学の世界において確率や割合は0〜100でなく、0〜1を使う場合が多いものの、人間からみれば前者の方が読みやすいかも知れない。

Code 22

table(pasta_df$Gender_D, pasta_df$Pasta) |>
  prop.table() |>
  addmargins() * 100

        
          Carbonara  MeatSauce  Naporitan Peperoncino        Sum
  Male    12.246696  17.709251  12.775330    9.251101  51.982379
  Female  12.246696  14.096916  13.480176    8.193833  48.017621
  Sum     24.493392  31.806167  26.255507   17.444934 100.000000

table(pasta_df$Over40_D, pasta_df$Pasta) |>
  prop.table() |>
  addmargins() * 100

          
            Carbonara  MeatSauce  Naporitan Peperoncino        Sum
  18 to 40  12.158590  15.594714  14.096916    5.726872  47.577093
  41 to 80  12.334802  16.211454  12.158590   11.718062  52.422907
  Sum       24.493392  31.806167  26.255507   17.444934 100.000000

　このような名目変数間の関係が独立しているかどうかを検定する\(\chi^2\)の検定は、クロス表をchisq.test()関数に渡すだけで実装できる。まずは性別と好きなパスタの関係を確認してみよう。

Code 23

table(pasta_df$Gender_D, pasta_df$Pasta) |>
  chisq.test()

    Pearson's Chi-squared test

data:  table(pasta_df$Gender_D, pasta_df$Pasta)
X-squared = 3.8204, df = 3, p-value = 0.2815

　検定統計量である\(\chi^2\)統計量は約3.820であり、\(p\)値は約0.282である。\(p\)値が一般的に採用される有意水準（\(\alpha = 0.05\)）以上であることから、性別と好きなパスタの間には関係性があるとは言えないという結論が得られた。年齢とパスタの関係はどうだろう。

Code 24

table(pasta_df$Over40_D, pasta_df$Pasta) |>
  chisq.test()

    Pearson's Chi-squared test

data:  table(pasta_df$Over40_D, pasta_df$Pasta)
X-squared = 22.515, df = 3, p-value = 5.095e-05

　検定統計量である\(\chi^2\)統計量は約22.515であり、\(p\)値は0.001未満である。\(p\)値が一般的に採用される有意水準（\(\alpha = 0.05\)）未満であることから、年齢と好きなパスタの間には統計的に有意な関係があると結論づけることができる。ただし、「何かの関係がある」ことまでは分かっても、具体的にどのような関係があるかは、クロス表を見ながら解釈する必要がある。今回の例だと、41歳以上の人は40歳以下の人に比べ、ペペロンチーノを好む傾向があることが分かる。