第5回講義資料

統計的推定

スライド

新しいタブで開く

セットアップ

　今回使用するパッケージは{tidyverse}のみだ。データはinference_data.csvであり、LMSから入手できる。読み込んだデータはdfという名のオブジェクトとして作業環境内に格納しておこう。

Code 01
library(tidyverse) # pacman::p_load(tidyverse) でもOK
df <- read_csv("Data/inference_data.csv")

df
# A tibble: 2,746 × 4
      ID Female   Age Temp_Ishin
   <dbl>  <dbl> <dbl>      <dbl>
 1     1      0    44         NA
 2     2      1    32         50
 3     3      1    53         20
 4     4      1    22          0
 5     5      1    27         NA
 6     6      1    28         NA
 7     7      0    28         30
 8     8      1    45         NA
 9     9      1    33         50
10    10      0    30         NA
# ℹ 2,736 more rows

　dfは2773行4列のデータであり、2021年9月に実施された世論調査の一部である。IDは回答者の識別番号、Femaleは女性ダミー変数（つまり、女性なら1、それ以外なら0）、Ageは回答者の年齢、Temp_Ishinは日本維新の会に対する感情温度であり、0なら嫌い、100なら好きを意味する。

母平均の推定

　まず、母集団（日本人の有権者全体）における維新感情温度の平均値（=母平均）を推定してみよう。母平均の一致推定量&不偏推定量は標本平均（\(\bar{x}\)）である。したがって、Temp_Ishin変数の平均値を計算するだけで、日本人有権者における維新感情温度の平均値が推定できる。ちなみにTemp_Ishinには欠損値が含まれているため、平均値を計算する際、na.rm = TRUEを忘れないこと。また、今後の分析のためにTemp_Ishinの標本分散（不偏分散; \(s^2\)）と有効ケース数（\(n\)）も計算しておこう。計算結果はsum_statという名のオブジェクトとして格納しておく。

Code 02
sum_stat <- df |>
  summarise(Mean = mean(Temp_Ishin, na.rm = TRUE),
            Var  = var(Temp_Ishin, na.rm = TRUE),
            N    = sum(!is.na(Temp_Ishin)))

sum_stat
# A tibble: 1 × 3
   Mean   Var     N
  <dbl> <dbl> <int>
1  42.7  569.  1998

　標本平均は42.733である。これは母集団（日本人の有権者）における維新感情温度の平均値の点推定値が42.733度であることを意味する。しかし、点推定値には常に不確実性が伴う。私たちがもう一回（2021年9月に戻って）同じやり方で2015名を対象とした世論調査を行えば、その時の点推定値（=標本平均）は異なるだろう。この点推定値（=標本平均）の不確実性を示す指標が標準誤差である。標準誤差は\(\sqrt{\frac{s^2}{n}}\)、あるいは\(\frac{s}{\sqrt{n}}\)で計算できる。sum_statに標準誤差をSEという名の列としてN列の前に追加し、sum_statを上書きする。

Code 03
sum_stat <- sum_stat |>
  mutate(SE      = sqrt(Var / N),
         .before = N)

sum_stat
# A tibble: 1 × 4
   Mean   Var    SE     N
  <dbl> <dbl> <dbl> <int>
1  42.7  569. 0.534  1998

　標準誤差は約0.534であるが、これだけだとどう解釈すれば良いかが分からないかも知れない（ある程度統計学に慣れたら標準誤差だけでも色々な考察ができるようになる）。標準誤差を使って、95%信頼区間を計算してみよう。95%信頼区間を計算するためには「（1）自由度の\(t\)分布において\(T\)統計量が\(t\)以下の値を取る確率が2.5%である\(t\)の値（\(t_{1997, 0.025}\)）」と「（2）自由度の\(t\)分布において\(T\)統計量が\(t\)以上の値を取る確率が2.5%である\(t\)の値（\(t_{1997, 0.975}\)）」を計算する必要がある。使用する確率分布は\(t\)分布であるため、qt()関数を使う。

　まず、「（1）自由度の\(t\)分布において\(T\)統計量が\(t\)以下の値を取る確率が2.5%である\(t\)の値」から計算してみよう。qt()の第一引数として0.025を指定する。これは2.5%を意味する。続いて、df引数に\(t\)分布の自由度を指定する。自由度はTemp_Ishinの有効ケース数（\(n\)）から1を引いた値だ。

Code 04
qt(0.025, df = sum_stat$N - 1)
[1] -1.961153

　得られた値は約-1.961である。これは自由度の\(t\)分布において\(T\)統計量が-1.961以下の値を取る確率が2.5%であることを意味する。

　つづいて、「（2）自由度の\(t\)分布において\(T\)統計量が\(t\)以上の値を取る確率が2.5%である\(t\)の値」から計算してみよう。これは逆にいうと「\(T\)統計量が\(t\)以上の値を取る確率が97.5%である\(t\)の値」とも解釈できる。したがって、qt()の第一引数として0.975を指定する。

Code 05
qt(0.975, df = sum_stat$N - 1)
[1] 1.961153

　得られた値は約1.961である。これは自由度の\(t\)分布において\(T\)統計量が1.961以上の値を取る確率が2.5%であることを意味する。

　95%信頼区間の下限は\(\bar{x} + t_{1997, 0.025} \cdot \mbox{SE}\)、上限は\(\bar{x} + t_{1997, 0.975} \cdot \mbox{SE}\)で計算できる（詳細はスライド参照）。それぞれCI_lower、CI_upperという名の列としてN列前に追加し、sum_statを上書きする。

Code 06
sum_stat <- sum_stat |>
  mutate(CI_lower = Mean + qt(0.025, df = N - 1) * SE,
         CI_upper = Mean + qt(0.975, df = N - 1) * SE,
         .before  = N)

sum_stat
# A tibble: 1 × 6
   Mean   Var    SE CI_lower CI_upper     N
  <dbl> <dbl> <dbl>    <dbl>    <dbl> <int>
1  42.7  569. 0.534     41.7     43.8  1998

　小数点を含めた詳しい値を確認してみよう。

Code 07
sum_stat$Mean # 母平均の一致＆不偏推定量（標本平均）
[1] 42.73273
Code 08
sum_stat$SE # 標準誤差（標本平均の不確実性）
[1] 0.5338369
Code 09
sum_stat$CI_lower # 95%信頼区間の下限
[1] 41.6858
Code 10
sum_stat$CI_upper # 95%信頼区間の上限
[1] 43.77967

　以上の計算により、標本平均は42.733、95%信頼区間は[41.686, 43.780]であることが分かる。

　以上の手順はパイプ演算子を複数つなげることで、dfから始まる一つのコードとしてまとめることもできる。複数のパイプ演算子をつなげていくためには、自分の頭の中で処理過程が想像できるようになる必要がある。学習段階では以上のようにステップごとにオブジェクトとして格納し、確認しながら分析を進めることが良いだろう。

Code 11
# オブジェクトとして格納せず、結果だけを出力
df |>
  summarise(Mean = mean(Temp_Ishin, na.rm = TRUE),
            Var  = var(Temp_Ishin, na.rm = TRUE),
            N    = sum(!is.na(Temp_Ishin))) |>
  mutate(SE       = sqrt(Var / N),
         t        = Mean / SE,
         CI_lower = Mean + qt(0.025, df = N - 1) * SE,
         CI_upper = Mean + qt(0.975, df = N - 1) * SE,
         .before  = N)
# A tibble: 1 × 7
   Mean   Var    SE     t CI_lower CI_upper     N
  <dbl> <dbl> <dbl> <dbl>    <dbl>    <dbl> <int>
1  42.7  569. 0.534  80.0     41.7     43.8  1998

t.test()の使い方

　母平均の推定について学習する場合、これまでのように一つ一つ計算しながら結果を確認する方法が望ましいが、実際にはt.test()という便利な関数を使う。指定する引数は2つであり、第一引数は母平均を推定するベクトル名、第二引数はconf.levelであり、算出する信頼区間を指定する。95%信頼区間の場合、0.95で良い。ちなみにconf.levelの既定値は0.95であるため、95%信頼区間を計算する場合は省略可能である。

Code 12
# 95%信頼区間を出すのであれば、 t.test(df$Temp_Ishin) だけでもOK
t.test(df$Temp_Ishin, conf.level = 0.95)

    One Sample t-test

data:  df$Temp_Ishin
t = 80.048, df = 1997, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 41.68580 43.77967
sample estimates:
mean of x 
 42.73273

　手計算（？）と同じ結果が得られることが分かる。

付録）95%信頼区間の意味

　ここでは95%信頼区間の意味をシミュレーションで確認してみよう。100人のクラスを想定し、このクラスを母集団とする。そして我々が知りたいのは100人の平均成績だとする。まずは、架空のデータを作ってみよう。コードの意味は説明しないが、100人の学生IDと成績が格納されたclass_dfという名のデータフレームが作られる。

set.seed(1986)
class_df <- tibble(ID = 1:100, Score = rnorm(100, 50, 10))
class_df
# A tibble: 100 × 2
      ID Score
   <int> <dbl>
 1     1  49.5
 2     2  52.8
 3     3  52.5
 4     4  40.4
 5     5  54.9
 6     6  43.0
 7     7  58.2
 8     8  42.9
 9     9  34.3
10    10  38.7
# ℹ 90 more rows

　この100人の成績が我々が本当に知りたいパラメーター（真の値）であり、それが50.96141点だ。

mean(class_df$Score) # 母集団におけるScoreの平均値
[1] 50.96141

　ここから30人を無作為抽出（復元抽出）してみよう。{dplyr}のslice_sample()関数を使えば簡単だ。30人を抽出する場合はn = 30を指定し、復元抽出を行うためにreplace = TRUEも付ける（既定値はreplace = FALSE）。抽出済みデータはtemp_class_dfと名付ける。

temp_class_df <- class_df |> 
  slice_sample(n = 30, replace = TRUE)

temp_class_df
# A tibble: 30 × 2
      ID Score
   <int> <dbl>
 1    33  52.7
 2    44  59.7
 3    78  49.4
 4    40  57.9
 5    98  49.1
 6    94  56.8
 7    49  42.4
 8    84  34.7
 9    88  54.3
10    36  50.2
# ℹ 20 more rows

　class_dfから30人のデータ（標本）が無作為抽出（復元抽出）された。この標本における成績の平均値（標本平均）はいくらだろうか。

mean(temp_class_df$Score)
[1] 48.7426

　48.7426という結果が得られた。母集団における平均値が50.96141点だから、偏り（バイアス）は2.21881（=\(|48.7426 - 50.96141|\)）だ。この偏りはいわゆる「誤差の範囲内」と言えるだろうか。t.test()を使用し、平均値だけでなく、95%信頼区間も求めてみよう。

t.test(temp_class_df$Score)

    One Sample t-test

data:  temp_class_df$Score
t = 27.934, df = 29, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 45.17389 52.31132
sample estimates:
mean of x 
  48.7426

　平均値は約48.7426、95%信頼区間の下限と上限はそれぞれ約45.17389、52.31132であることが分かった。そして、この区間内には母集団における成績の平均値（50.96141）が含まれている。標本平均と母平均間のズレ（バイアス）があるものの、これは誤差の範囲内とも言えよう。

　同じような作業をもう一度やってみよう。

temp_class_df <- class_df |> 
  slice_sample(n = 30, replace = TRUE)

temp_class_df
# A tibble: 30 × 2
      ID Score
   <int> <dbl>
 1    76  49.0
 2    31  33.2
 3    30  61.8
 4    59  45.2
 5     8  42.9
 6    33  52.7
 7    51  62.2
 8   100  34.2
 9    59  45.2
10    84  34.7
# ℹ 20 more rows

　上書きされたtemp_class_dfはclass_dfから新しく無作為抽出されたものであることが分かる。もう一度、temp_class_dfを使ってScore列の平均値と95%信頼区間を求めてみよう。

t.test(temp_class_df$Score)

    One Sample t-test

data:  temp_class_df$Score
t = 24.988, df = 29, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 45.39364 53.48703
sample estimates:
mean of x 
 49.44033

　平均値は約49.44033、95%信頼区間の下限と上限はそれぞれ約45.39364、53.48703であり、この区間内に50.96141が含まれている。もう一度同じことをやってみよう。

temp_class_df <- class_df |> 
  slice_sample(n = 30, replace = TRUE)

t.test(temp_class_df$Score)

    One Sample t-test

data:  temp_class_df$Score
t = 33.415, df = 29, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 49.44786 55.89568
sample estimates:
mean of x 
 52.67177

　以上の3回の結果をまとめたものが以下の表だ。

施行 平均値
95%信頼区間
95%信頼区間内に50.96141が
下限 上限
1 48.743 45.174 52.311 含まれる
2 49.440 45.394 53.487 含まれる
3 52.672 49.448 55.896 含まれる

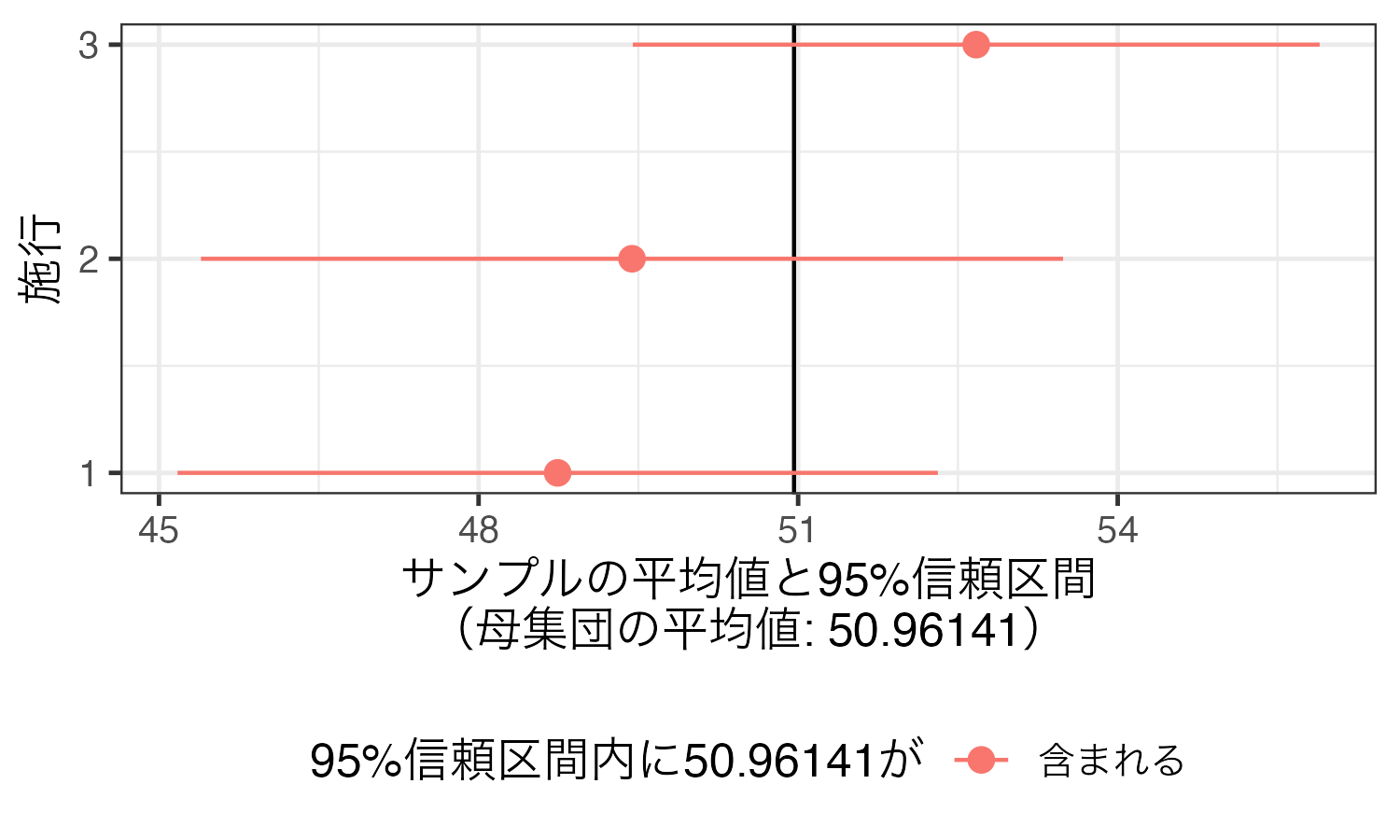
　以下は上記の表を可視化したものである。点が各施行における成績の平均値、水平線は95%信頼区間を意味する。黒い垂直線は100人の母集団における成績の平均値（50.96141点）である。いずれも母集団の平均値（パラメーター）が含まれていることが分かる。

　この作業を3回でなく、10回やってみよう。以下のコードは理解できなくても良い。大事なのは、これまでやったことを3回でなく、10回やるということだ。

temp_mean  <- c()
temp_lower <- c()
temp_upper <- c()

for (i in 1:10) {
  temp_class_df <- class_df |> 
  slice_sample(n = 30, replace = TRUE)
  
  temp_mean[i]  <- t.test(temp_class_df$Score)$estimate
  temp_lower[i] <- t.test(temp_class_df$Score)$conf.int[1]
  temp_upper[i] <- t.test(temp_class_df$Score)$conf.int[2]
}

sim_df <- tibble(trial = 1:10,
                 mean  = temp_mean,
                 lower = temp_lower,
                 upper = temp_upper)

sim_df
# A tibble: 10 × 4
   trial  mean lower upper
   <int> <dbl> <dbl> <dbl>
 1     1  53.3  49.1  57.5
 2     2  47.2  44.6  49.8
 3     3  49.1  45.3  52.9
 4     4  51.2  48.6  53.8
 5     5  50.5  46.9  54.0
 6     6  52.2  48.4  56.0
 7     7  51.2  46.7  55.7
 8     8  51.9  47.3  56.4
 9     9  53.8  50.5  57.0
10    10  52.9  49.2  56.5

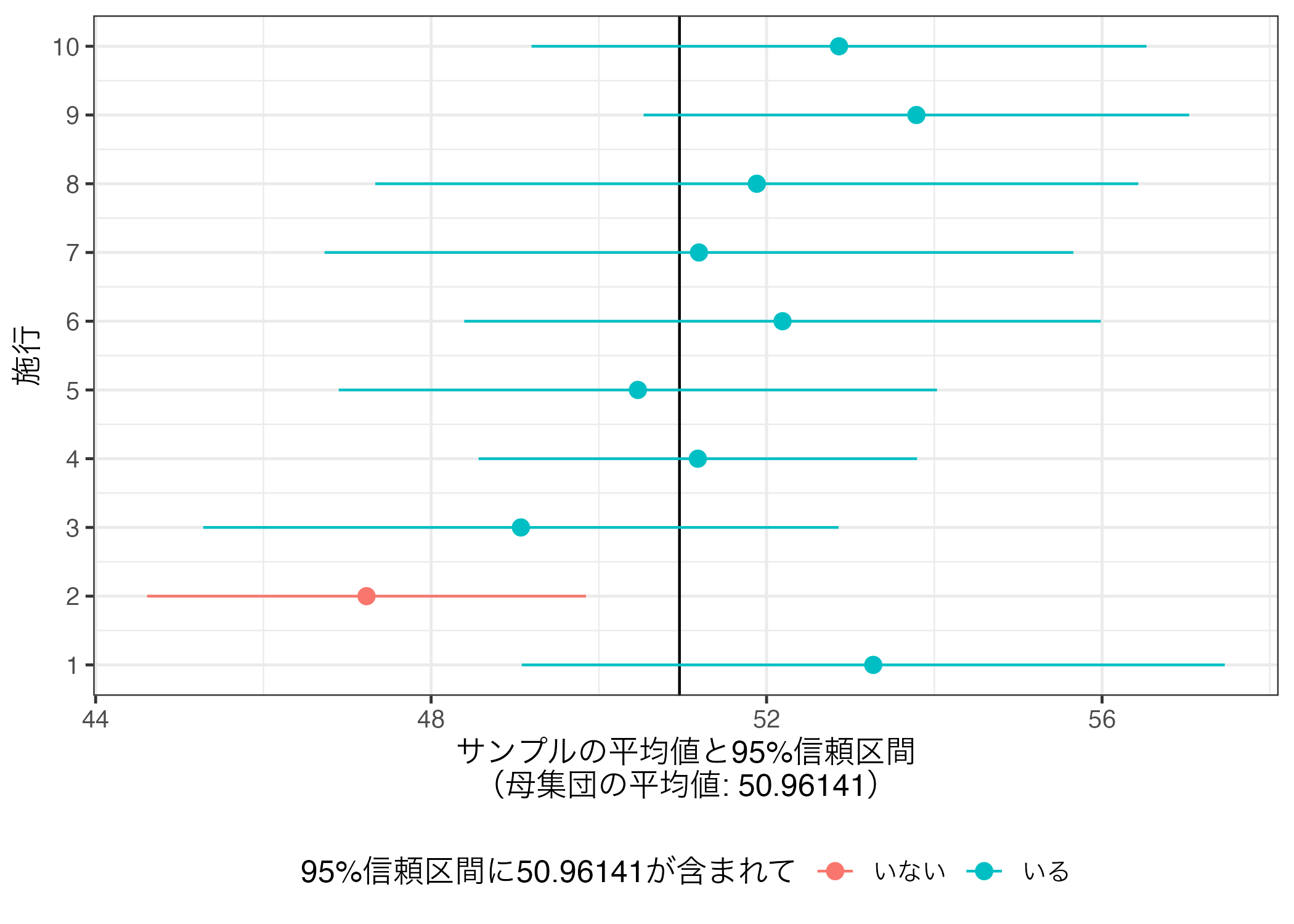
　2回目の施行では95%信頼区間が母集団の平均値を含まないが、残りの9回分では含まれていることが分かる。可視化したら以下のような図になる。

sim_df |> 
  mutate(inout = if_else(lower <= 50.96141 & upper >= 50.96141, "いる", "いない")) |> 
  ggplot() +
  geom_vline(xintercept = 50.96141) +
  geom_pointrange(aes(y = trial, x = mean, xmin = lower, xmax = upper, color = inout)) +
  labs(x = "サンプルの平均値と95%信頼区間\n（母集団の平均値: 50.96141）", y = "施行",
       color = "95%信頼区間に50.96141が含まれて") +
  scale_y_continuous(breaks = 1:10, labels = 1:10) +
  theme_bw(base_size = 12) +
  theme(legend.position = "bottom")

　100回ならどうだろう。

temp_mean  <- c()
temp_lower <- c()
temp_upper <- c()

for (i in 1:100) {
  temp_class_df <- class_df |> 
  slice_sample(n = 30, replace = TRUE)
  
  temp_mean[i]  <- t.test(temp_class_df$Score)$estimate
  temp_lower[i] <- t.test(temp_class_df$Score)$conf.int[1]
  temp_upper[i] <- t.test(temp_class_df$Score)$conf.int[2]
}

sim_df <- tibble(trial = 1:100,
                 mean  = temp_mean,
                 lower = temp_lower,
                 upper = temp_upper)

sim_df
# A tibble: 100 × 4
   trial  mean lower upper
   <int> <dbl> <dbl> <dbl>
 1     1  48.5  44.7  52.2
 2     2  52.0  48.2  55.8
 3     3  50.1  46.1  54.2
 4     4  50.7  46.5  54.9
 5     5  50.2  46.0  54.4
 6     6  50.7  46.7  54.7
 7     7  51.2  47.8  54.6
 8     8  52.9  48.6  57.1
 9     9  49.1  45.3  52.9
10    10  51.0  47.9  54.1
# ℹ 90 more rows
sim_df |> 
  mutate(inout = if_else(lower <= 50.96141 & upper >= 50.96141, "いる", "いない")) |> 
  ggplot() +
  geom_vline(xintercept = 50.96141) +
  geom_pointrange(aes(y = trial, x = mean, xmin = lower, xmax = upper, color = inout)) +
  labs(x = "サンプルの平均値と95%信頼区間\n（母集団の平均値: 50.96141）", y = "施行",
       color = "95%信頼区間に50.96141が含まれて") +
  theme_bw(base_size = 12) +
  theme(legend.position = "bottom")

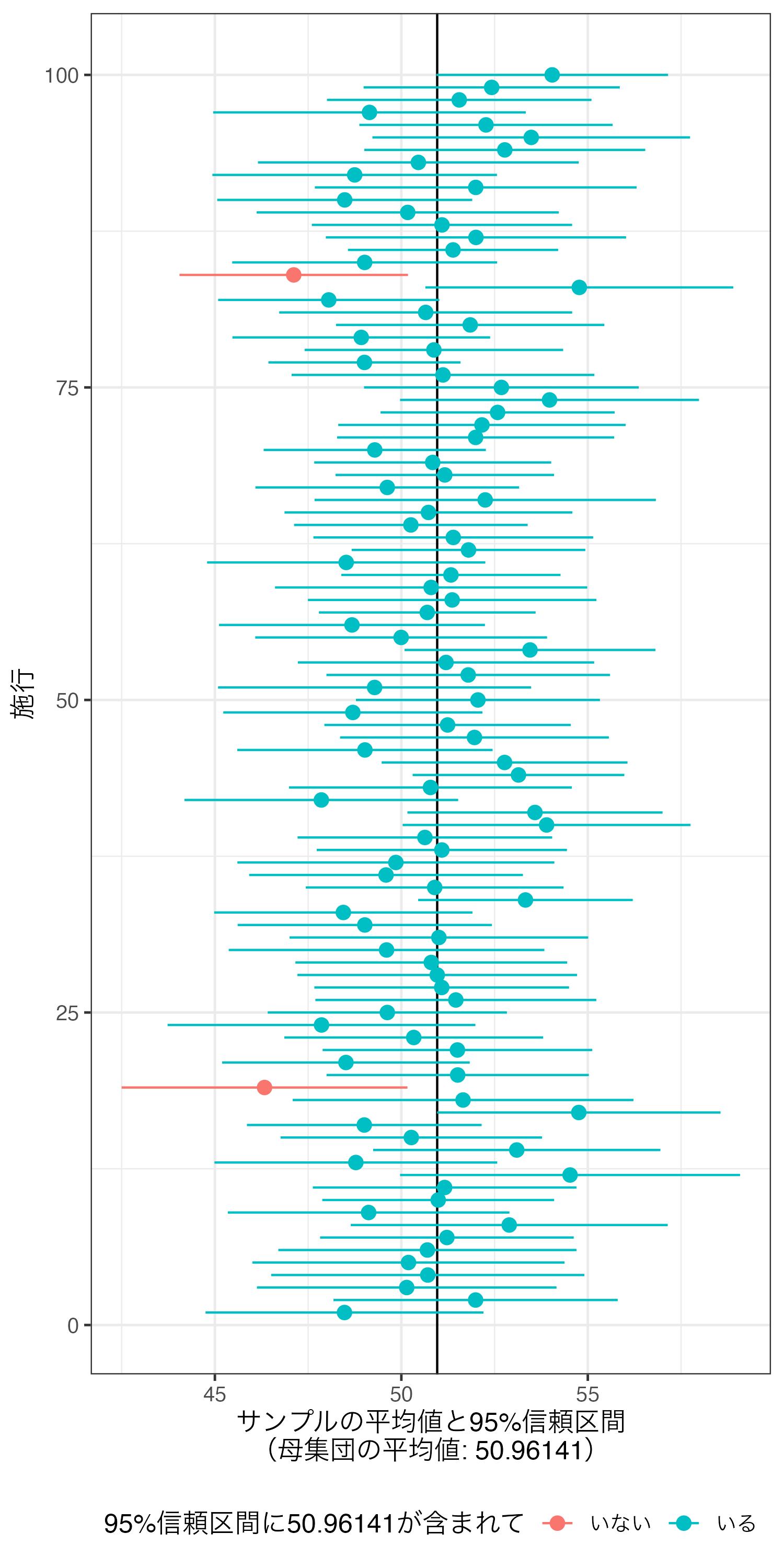
　95%信頼区間に母集団の平均値が含まれていない施行は2回だけである。これが100回でなく、10000回になったらどうだろうか。以下はその結果である。

temp_mean  <- c()
temp_lower <- c()
temp_upper <- c()

for (i in 1:10000) {
  temp_class_df <- class_df |> 
  slice_sample(n = 30, replace = TRUE)
  
  temp_mean[i]  <- t.test(temp_class_df$Score)$estimate
  temp_lower[i] <- t.test(temp_class_df$Score)$conf.int[1]
  temp_upper[i] <- t.test(temp_class_df$Score)$conf.int[2]
}

sim_df <- tibble(trial = 1:10000,
                 mean  = temp_mean,
                 lower = temp_lower,
                 upper = temp_upper)

sim_df
# A tibble: 10,000 × 4
   trial  mean lower upper
   <int> <dbl> <dbl> <dbl>
 1     1  52.2  48.6  55.8
 2     2  50.8  47.7  53.8
 3     3  49.4  45.8  52.9
 4     4  50.6  47.2  54.1
 5     5  49.9  46.9  53.0
 6     6  48.6  44.8  52.4
 7     7  48.1  44.3  51.8
 8     8  51.4  48.1  54.7
 9     9  48.1  45.5  50.8
10    10  49.1  45.5  52.6
# ℹ 9,990 more rows

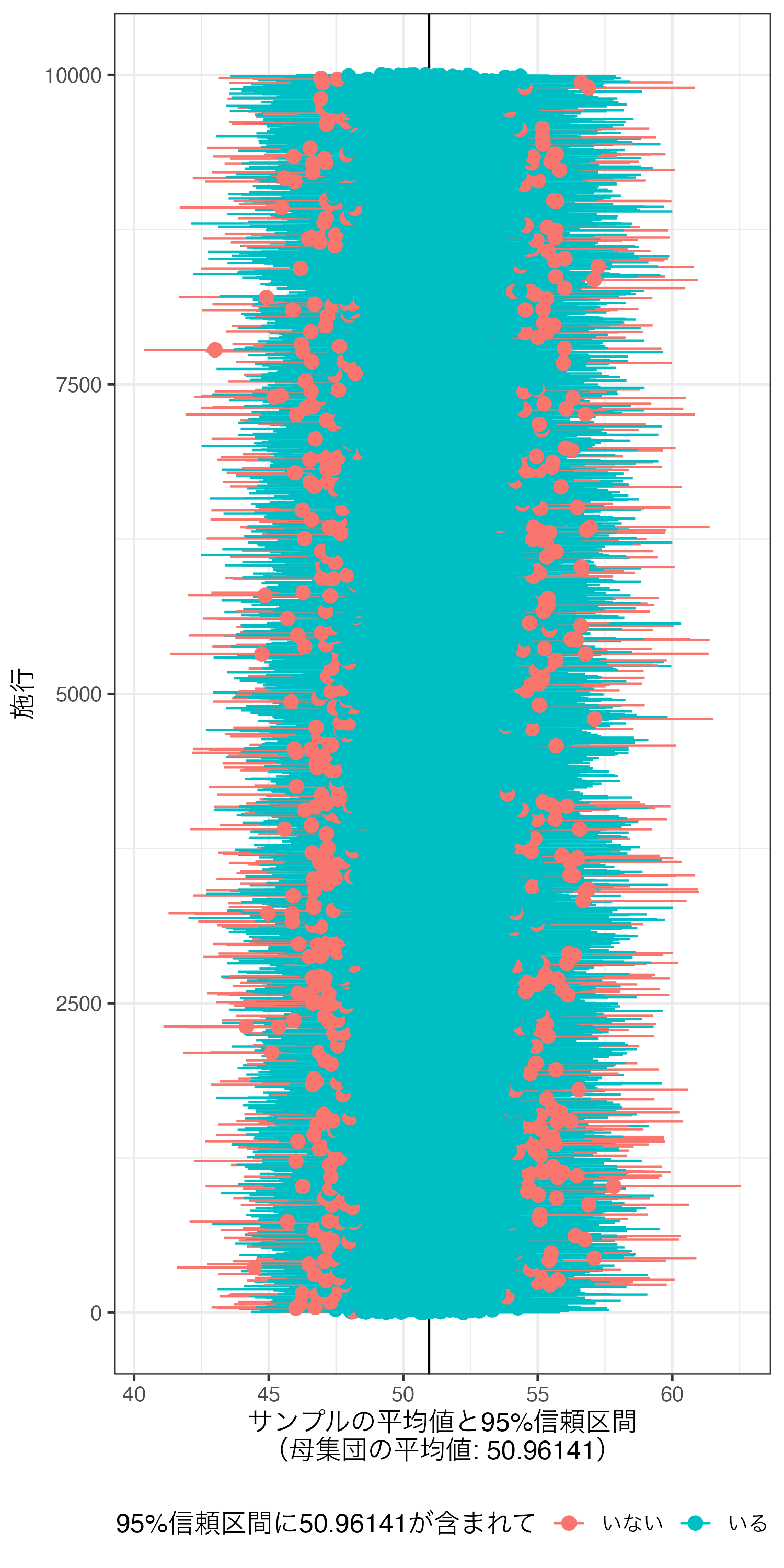
　1万本のPoint-rangeが並んでいるため、95%信頼区間が母集団の平均値を含む施行が何回あったのかは図からは分かりにくい。

sim_df |> 
  mutate(inout = if_else(lower <= 50.96141 & upper >= 50.96141, "いる", "いない")) |> 
  ggplot() +
  geom_vline(xintercept = 50.96141) +
  geom_pointrange(aes(y = trial, x = mean, xmin = lower, xmax = upper, color = inout)) +
  labs(x = "サンプルの平均値と95%信頼区間\n（母集団の平均値: 50.96141）", y = "施行",
       color = "95%信頼区間に50.96141が含まれて") +
  theme_bw(base_size = 12) +
  theme(legend.position = "bottom")

　具体的に何回なのかを数えるのは実質不可能だから、直接計算するしかない。

sum(sim_df$lower <= 50.96141 & sim_df$upper >= 50.96141)
[1] 9492

　95%信頼区間に母集団の平均値が含まれている施行は計9492回である。割合から見ると94.9%だ。これが1万回でなく、無限回ならこの割合は95%になる。これが「95%の95%信頼区間にパラメーターが含まれている」ということの意味だ。逆に90%信頼区間であれば「90%の90%信頼区間にパラメーターが含まれている」ことになろう。