第13回講義資料

可視化 (2)

スライド

新しいタブで開く

グラフ作成の手順

　{ggplot2}を用いた作図は以下の手順で行われる。

1. 作成したいグラフを決める
2. 作成したいグラフの完成図を想像する or 描いてみる
3. グラフ上の要素（点、線、面）が持つ情報を考える
4. 3の情報が一つの変数（列）と対応するような整然データを作成する
5. {ggplot2}で作図
6. 図のカスタマイズ
7. 図の保存

　今回は第9回の実習用データ（countries.csv）を使用する。{tidyverse}パッケージを読み込んだ後、read_csv()関数でデータを読み込む。

Code 01

library(tidyverse)
df <- read_csv("Data/countries.csv")

棒グラフ

　まずは、棒グラフについて解説する。ここに紙と鉛筆があるとし、棒グラフを描くとしよう。棒グラフは適当なもので良い。棒グラフには通常、2つ以上の棒が並んでいる。それぞれの棒から我々は何が分かるだろうか。

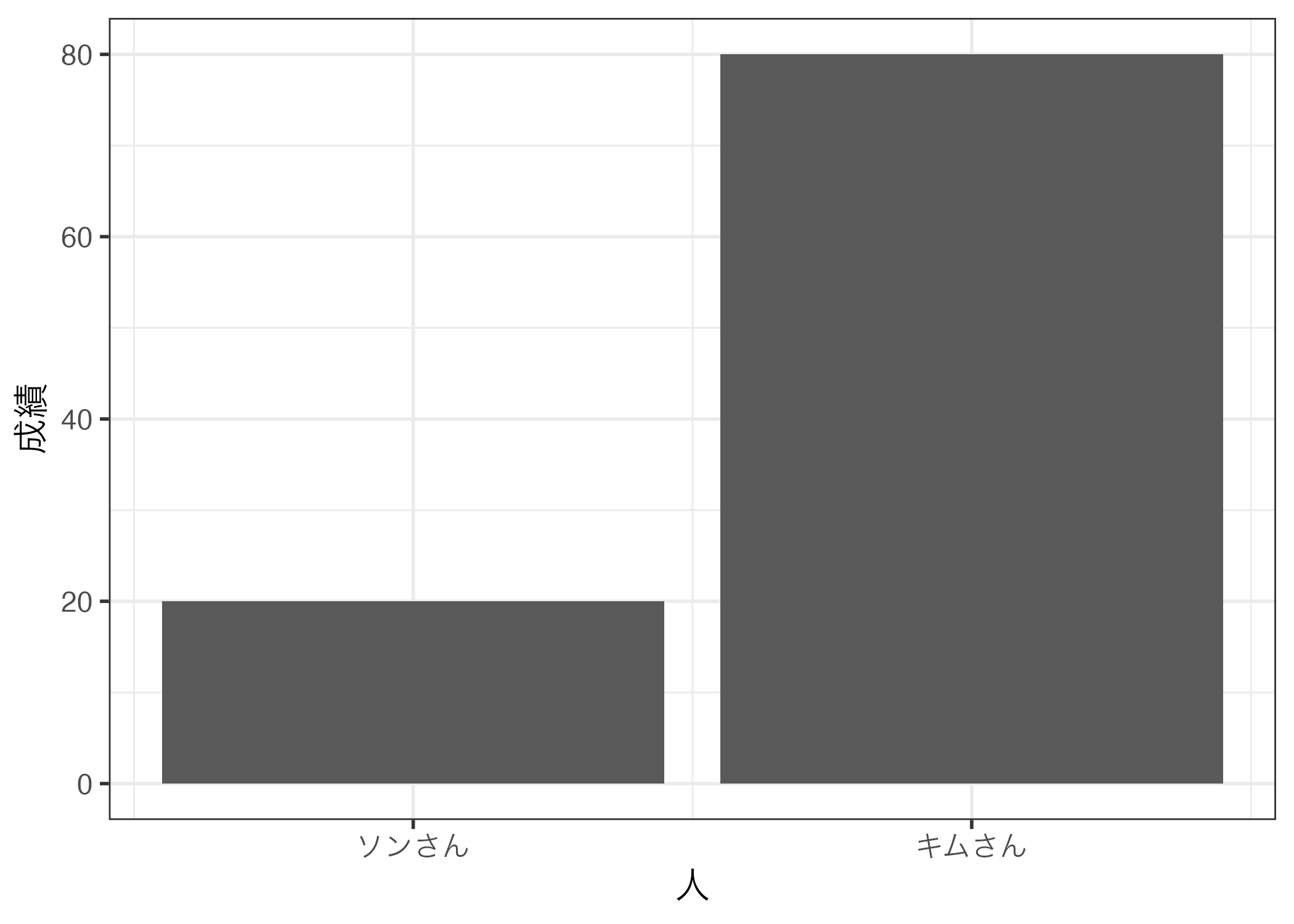
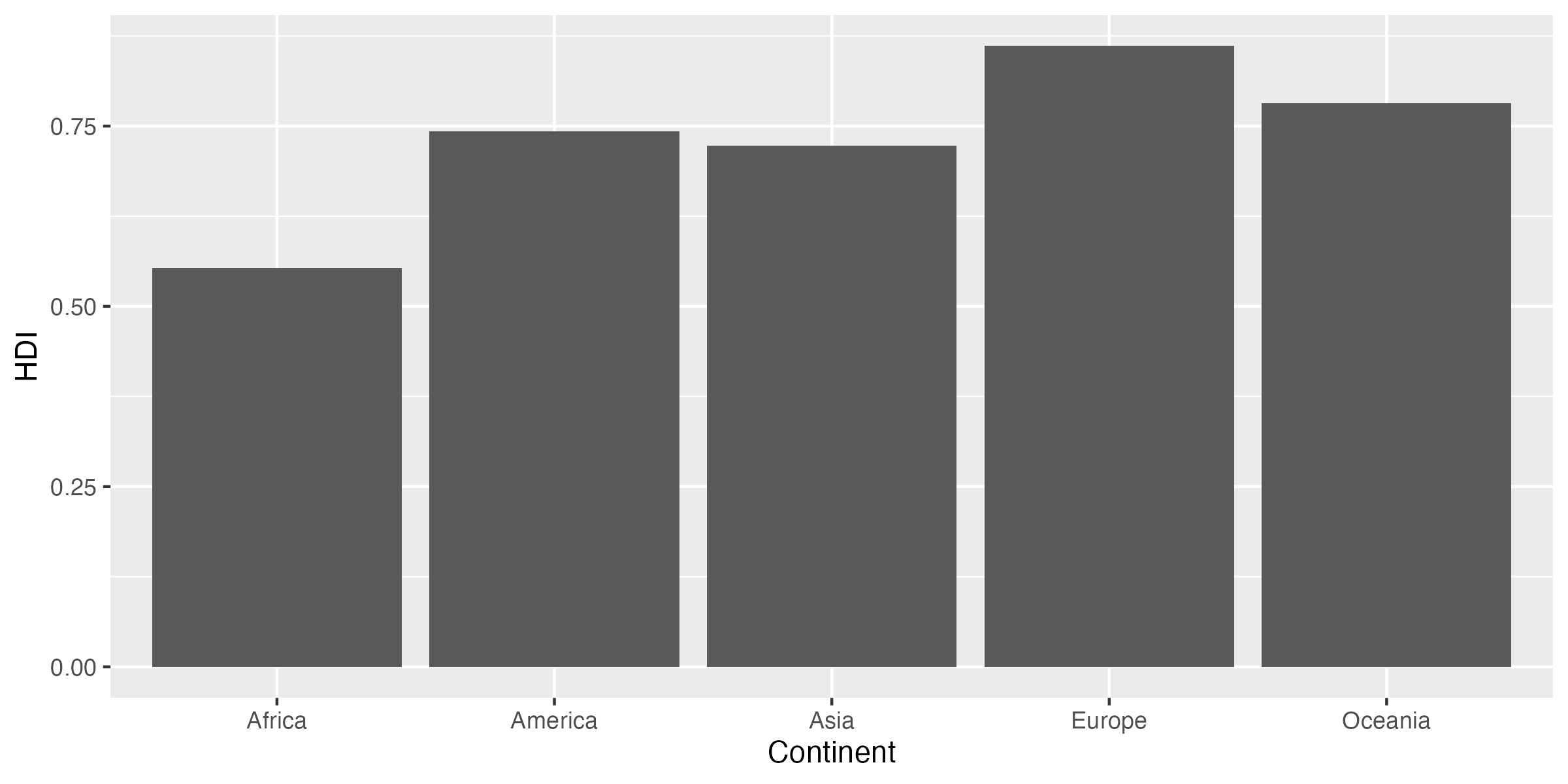
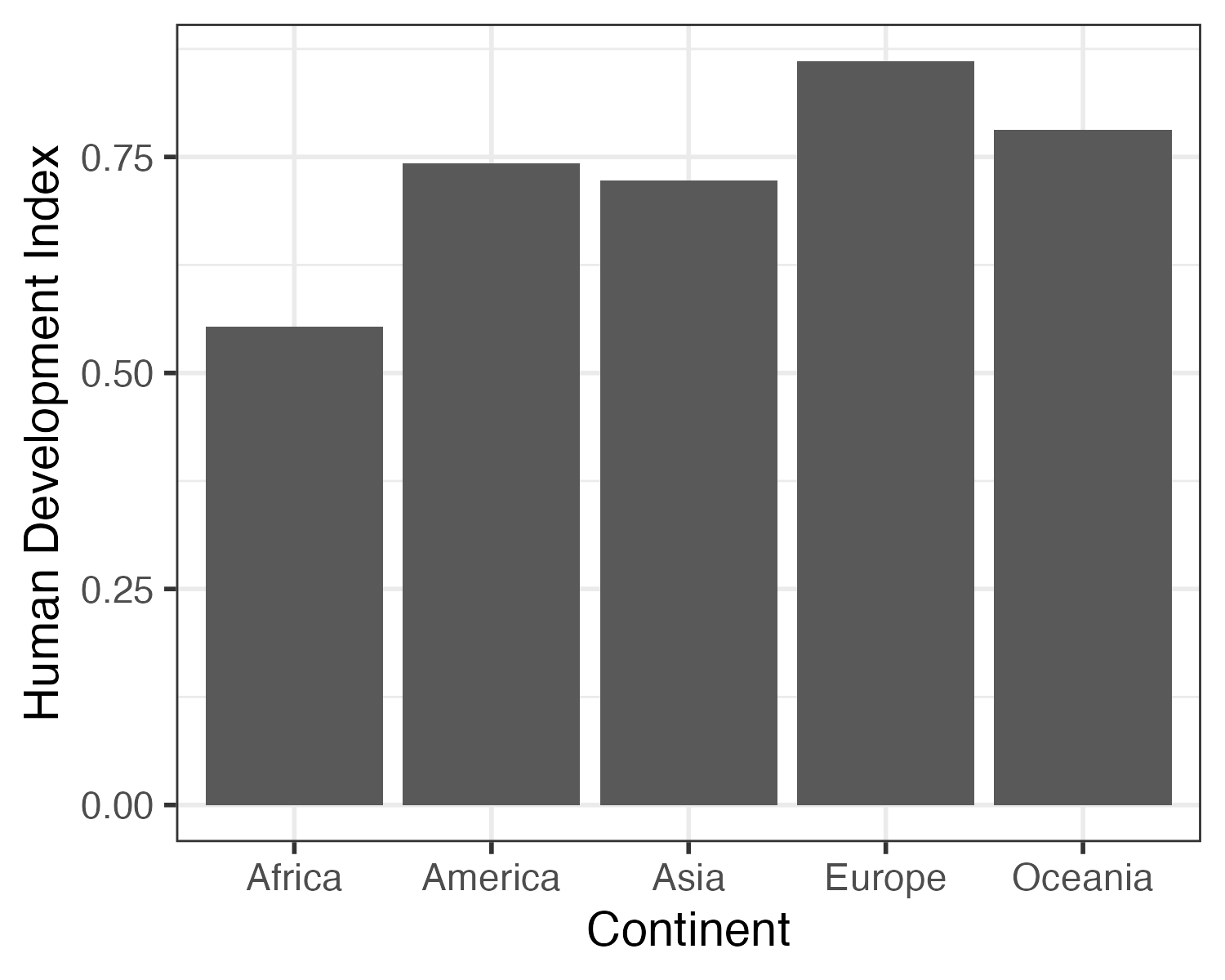
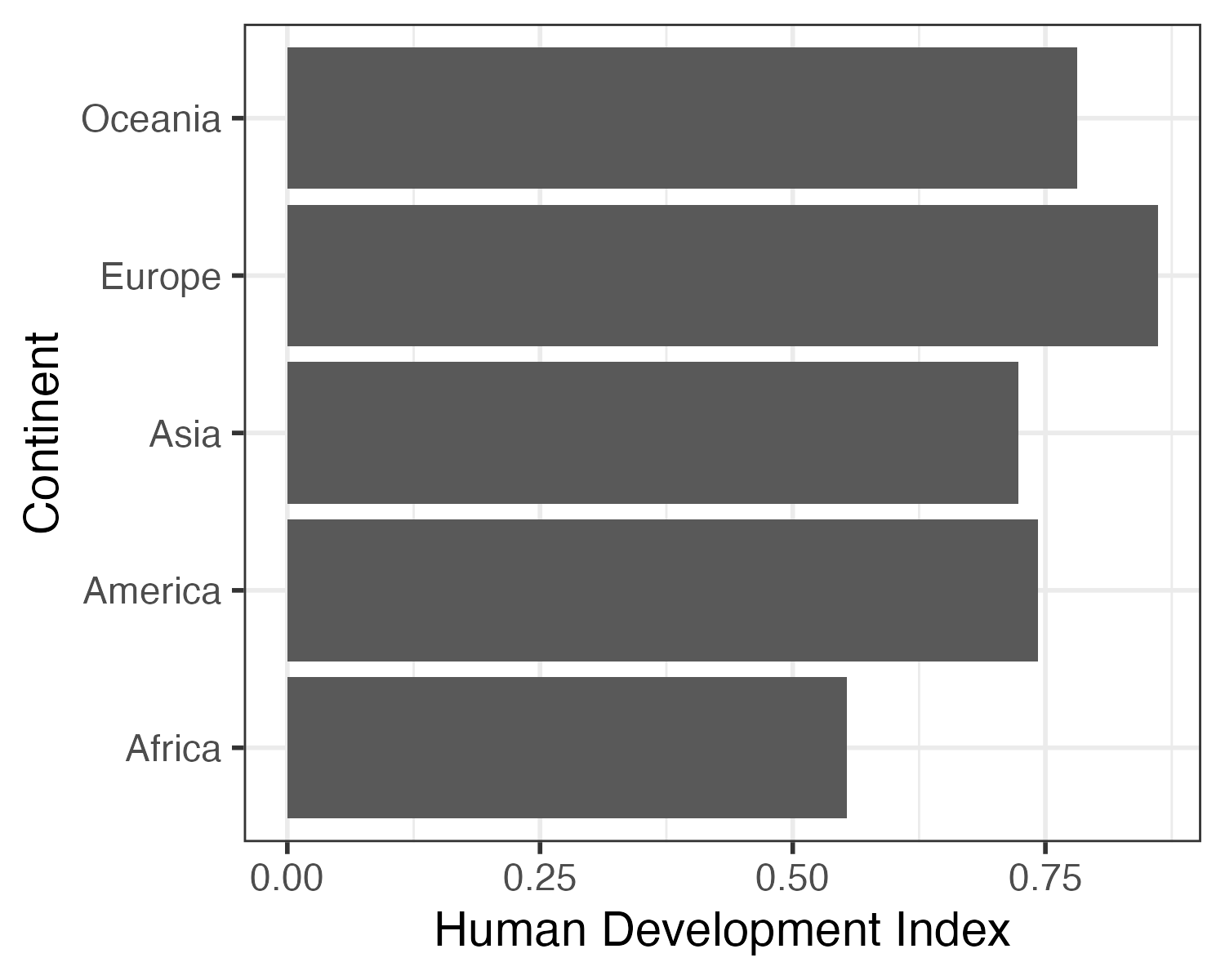
　この棒から分かるのは「ある人の成績」である。成績は棒の高さで分かり、それが誰の成績なのかは棒の横軸上の位置から分かる。つまり、棒グラフには棒の横軸上の位置、高さといった2つの次元で構成され、それぞれ人と成績に対応する。この位置と高さは棒グラフを作成する際に必要な最低限の情報である。むろん、以下の 図 1 (b) のように位置を縦軸上の位置に、人間開発指数の平均値を棒の長さとして定義することできる。いずれにせよ、以下のような棒グラフを作成するためには「大陸」と「人間開発指数の平均値」といった2つの変数が必要だ。

(a) xが大陸、yが人間開発指数

(b) yが大陸、xが人間開発指数

図 1: 2つの棒グラフ

棒グラフの作成

　それではデータを作成してみよう。{dplyr}を使用し、大陸 (Continent)ごとの人間開発指数 (HDI_2018)の平均値を計算し、df2という名で格納しておく。

Code 02

df2 <- df |>
   group_by(Continent) |>
   summarise(HDI = mean(HDI_2018, na.rm = TRUE))

df2

# A tibble: 5 × 2
  Continent   HDI
  <chr>     <dbl>
1 Africa    0.553
2 America   0.742
3 Asia      0.723
4 Europe    0.861
5 Oceania   0.782

　棒グラフに必要な2つの変数が揃った。ただし、データがこの2つの変数のみで構成される必要はない。含まれていれば問題ない。それでは作図に移ろう。棒グラフを作成するときに使用する幾何オブジェクトgeom_col()である。また、aes()内に指定するマッピングは棒の横軸上の位置を意味するxと棒の高さを意味するyである。そして、棒の横軸上の位置は大陸（Continent）、棒の高さは人間開発指数の平均値（HDI）なので、マッピングはx = Continent, y = HDIとなる。もし、図 1 (b) のような図を作成するなら、xとyを逆にすれば良い。

　それでは図を作成しbar_plot1という名のオブジェクトとして格納しておこう。格納された図を出力する場合はオブジェクト名のみ入力すれば良い。

Code 03

bar_plot1 <- df2 |>
  ggplot() +
  geom_col(aes(x = Continent, y = HDI))

bar_plot1

　もし、論文・レポートの使用言語が日本語であるなら図表も日本語にする必要がある。bar_plot1を日本語にする場合、修正が必要な箇所は大陸名とそれぞれの軸のタイトルである。まず、df2のContinent列を日本語にリコーディングし、Continent_Jという名の列として追加する。

Code 04

df2 <- df2 |>
   mutate(Continent_J = case_when(Continent == "Asia"    ~ "アジア",
                                  Continent == "Africa"  ~ "アフリカ",
                                  Continent == "America" ~ "アメリカ",
                                  Continent == "Europe"  ~ "ヨーロッパ",
                                  TRUE                   ~ "オセアニア"))

df2

# A tibble: 5 × 3
  Continent   HDI Continent_J
  <chr>     <dbl> <chr>      
1 Africa    0.553 アフリカ   
2 America   0.742 アメリカ   
3 Asia      0.723 アジア     
4 Europe    0.861 ヨーロッパ 
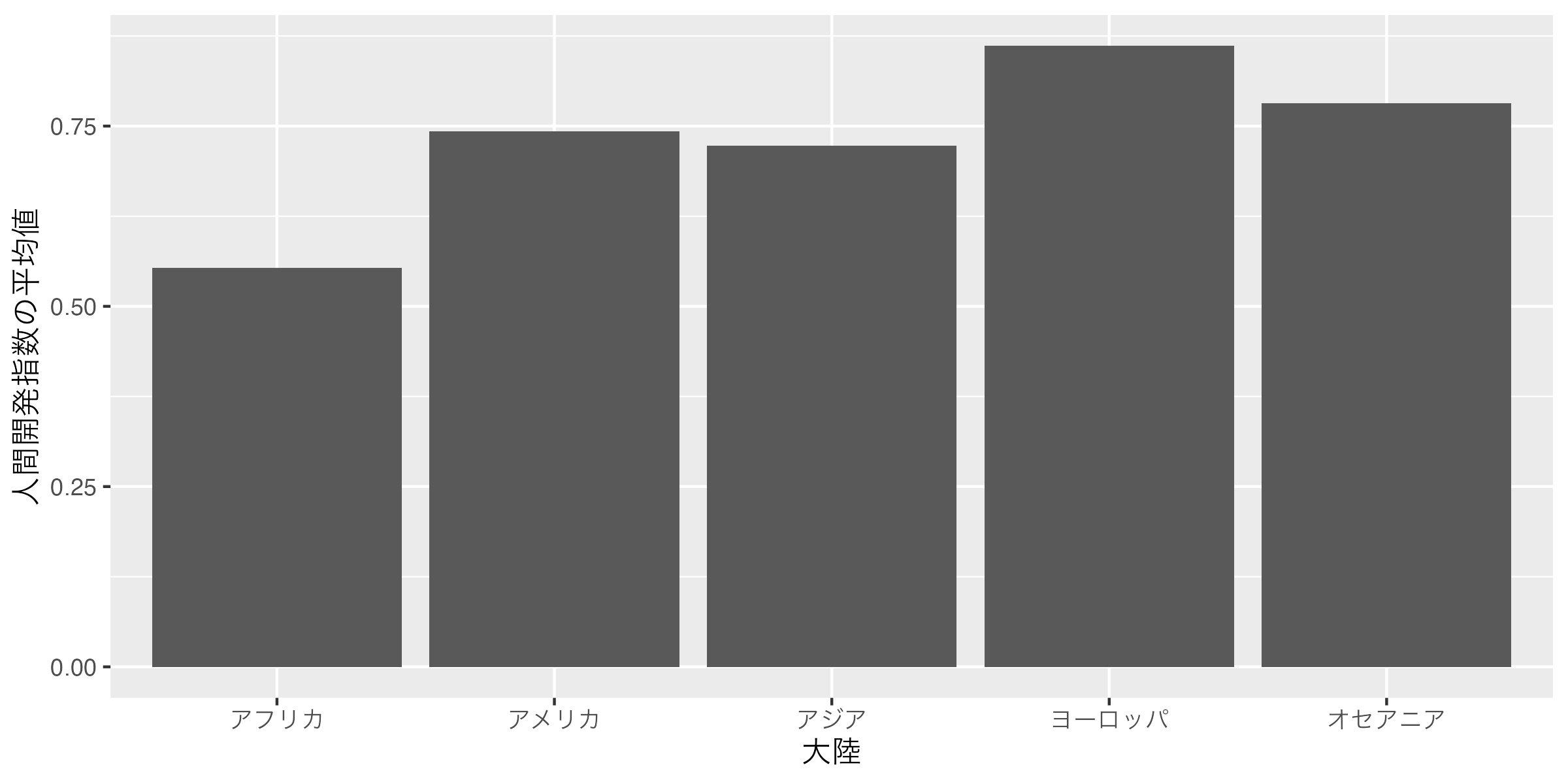
5 Oceania   0.782 オセアニア 

　作図の際、Continentの代わりにContinent_Jを使用する。また、X軸とY軸のタイトルを修正するためにlabs()レイヤーを追加し、軸のタイトルを指定する。

Code 05

df2 |>
   ggplot() +
   geom_col(aes(x = Continent_J, y = HDI)) +
   labs(x = "大陸", y = "人間開発指数の平均値")

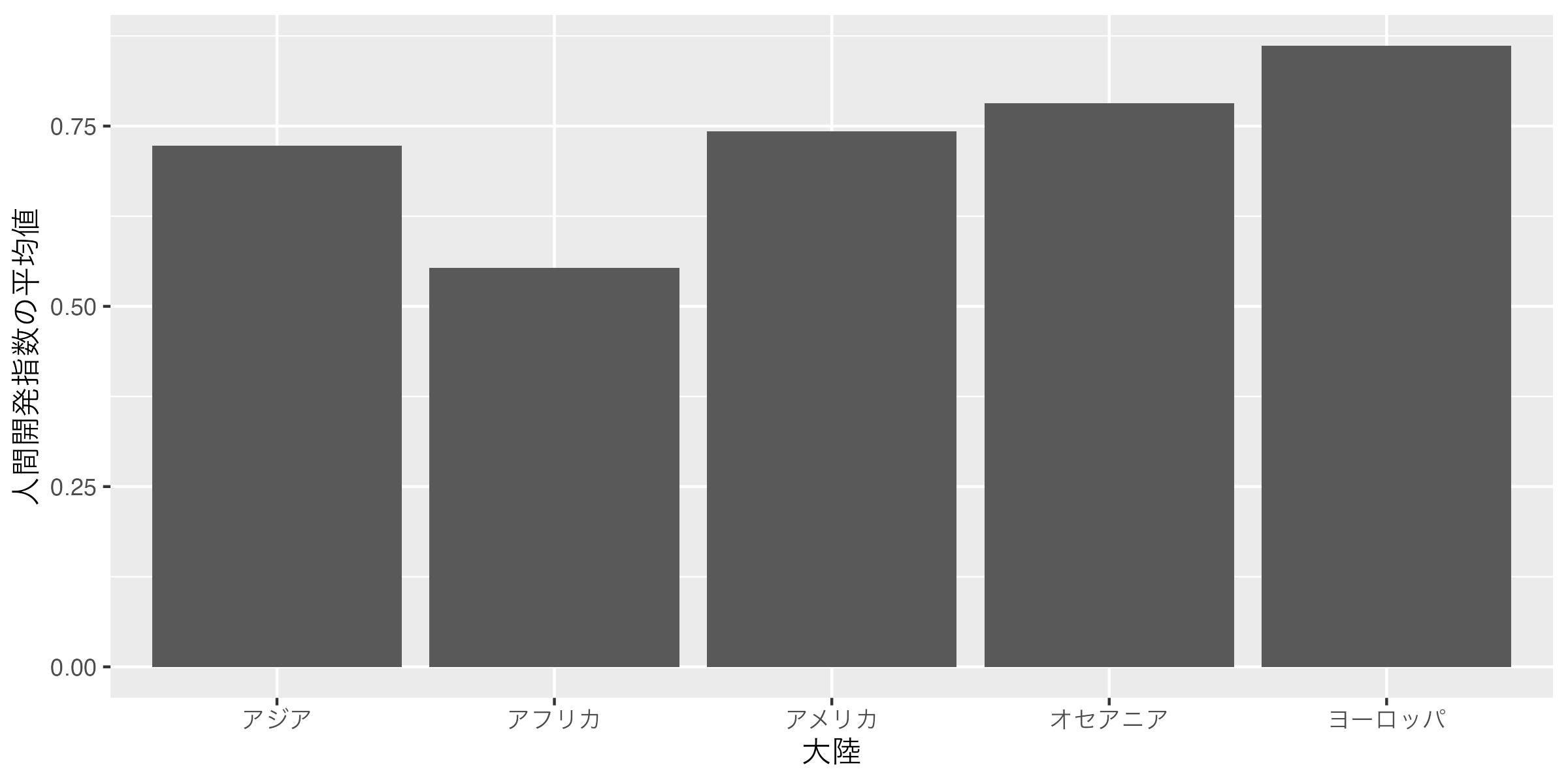
　JDCat分析ツールを使用する場合、以上のような図が得られるはずである。しかし、自分のPCにインストールしたR/RStudioを使用する場合、文字化けは生じる可能性がある。この場合、theme_*()レイヤーを追加し、引数としてbase_family = "日本語フォント"を指定する必要がある。theme_*()はtheme_で始まる関数の総称であり、theme_gray()（{ggplot2}のデフォルトテーマ）、theme_bw()、theme_minimal()などがある。日本語フォントは好きなものを使えば良いが、macOSの場合は"HiraginoSans-W3"、Windowsの場合は"Yu Gothic"が無難だろう。以下のコードはmacOSで文字化けが生じた場合のコードの改善例である。

Code 06

df2 |>
   ggplot() +
   geom_col(aes(x = Continent_J, y = HDI)) +
   labs(x = "大陸", y = "人間開発指数の平均値") +
   theme_gray(base_family = "HiraginoSans-W3")

　先ほどのグラフを見ると、大陸がアジア、アフリカ、アメリカ、オセアニア、ヨーロッパ順となっている。これをアルファベット順に並べ替える、つまり、アフリカ、アメリカ、アジア、ヨーロッパ、オセアニアの順番にするにはどうすれば良いだろうか。答えはContinet_J列をfactor化し、アフリカ、アメリカ、アジア、ヨーロッパ、オセアニア順にすることだ。df2をggplot()関数に渡す前にmutate()を入れ、そこでContinent_J列をfactor化すれば良い。

Code 07

df2 |>
   mutate(Continent_J = factor(Continent_J, 
                               levels = c("アフリカ", "アメリカ", "アジア", 
                                          "ヨーロッパ", "オセアニア"))) |> 
   ggplot() +
   geom_col(aes(x = Continent_J, y = HDI)) +
   labs(x = "大陸", y = "人間開発指数の平均値") +
   theme_bw() # Black and Whiteテーマも使ってみよう

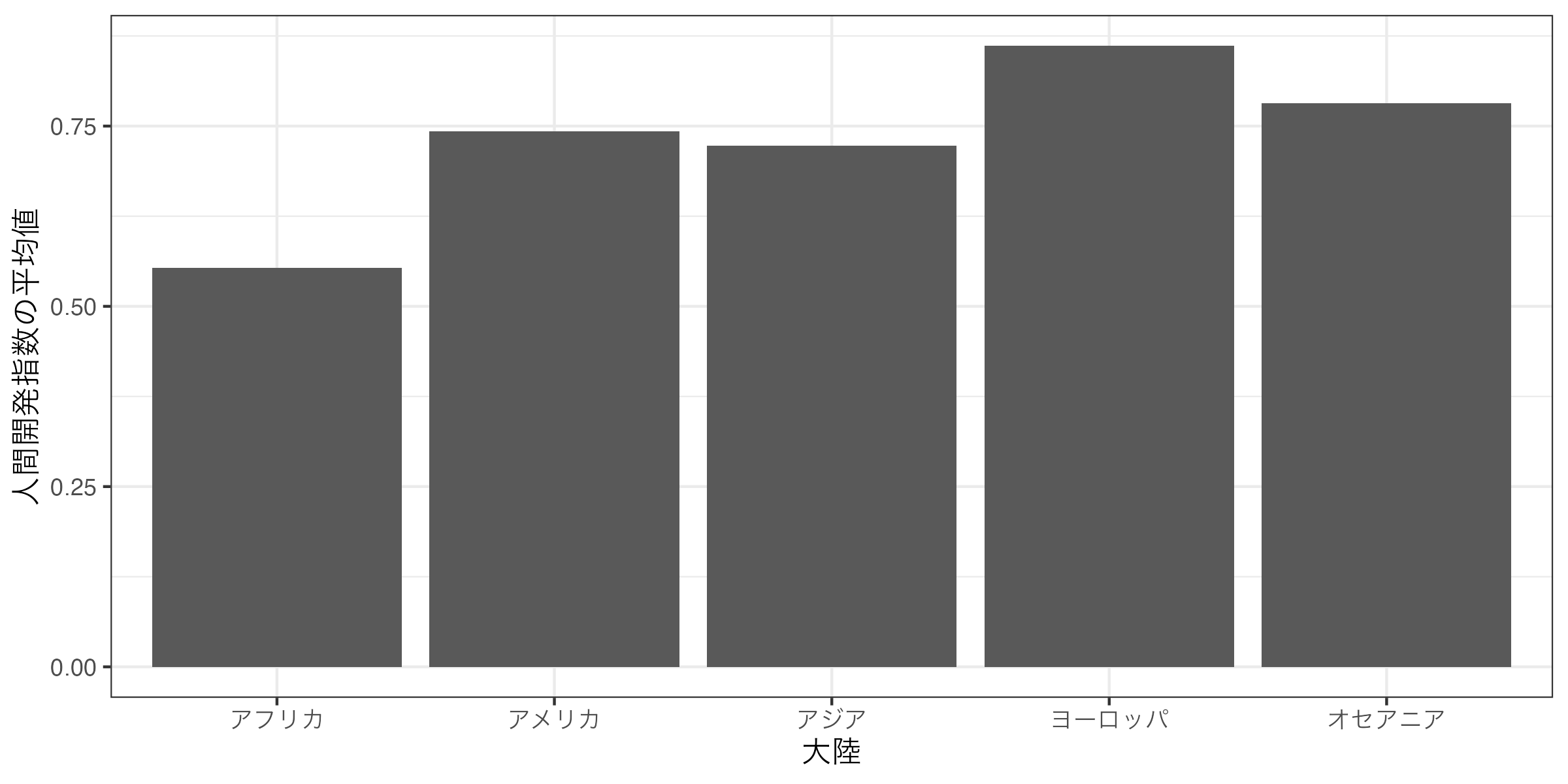
　ただし、df2を見ると表の順番はアルファベット順になっている。

Code 08

df2

# A tibble: 5 × 3
  Continent   HDI Continent_J
  <chr>     <dbl> <chr>      
1 Africa    0.553 アフリカ   
2 America   0.742 アメリカ   
3 Asia      0.723 アジア     
4 Europe    0.861 ヨーロッパ 
5 Oceania   0.782 オセアニア 

　このように表で表示されている順番は作図の際の順番は一致しない場合がある。この順番を調整するためには、当該変数を予めfactor化しておく必要がある。

　ここで一つ便利な関数を紹介しよう。それはfct_inorder()関数だ。この関数は{forcats}パッケージに含まれている関数であり、{tidyverse}を読み込む際、一緒に読み込まれるので{tidyverse}を読み込んだら別途読み込む必要はない。このfct_inorder()は()内の変数をfactor化し、各要素順番を表で登場した順番にしてくれる関数だ。現在、df2はアルファベット順になっているので、この表の順番通りにContinent_Jの要素の順番が固定される。

Code 09

df2 |>
   mutate(Continent_J = fct_inorder(Continent_J)) |>
   ggplot() +
   geom_col(aes(x = Continent_J, y = HDI)) +
   labs(x = "大陸", y = "人間開発指数の平均値")

次元の追加

　通常の棒グラフはX軸とY軸のみで構成される2次元グラフである。棒グラフ上の棒には「ある大陸 (X軸) のHDIの平均値 (Y軸)」といった2つの情報が含まれている。つまり、一部の例外を除き、グラフの次元数は情報量を意味し、これは{ggplot2}の幾何オブジェクト内のaes()内で指定する引数の数でもある。以下では次元を増やす方法について紹介する。

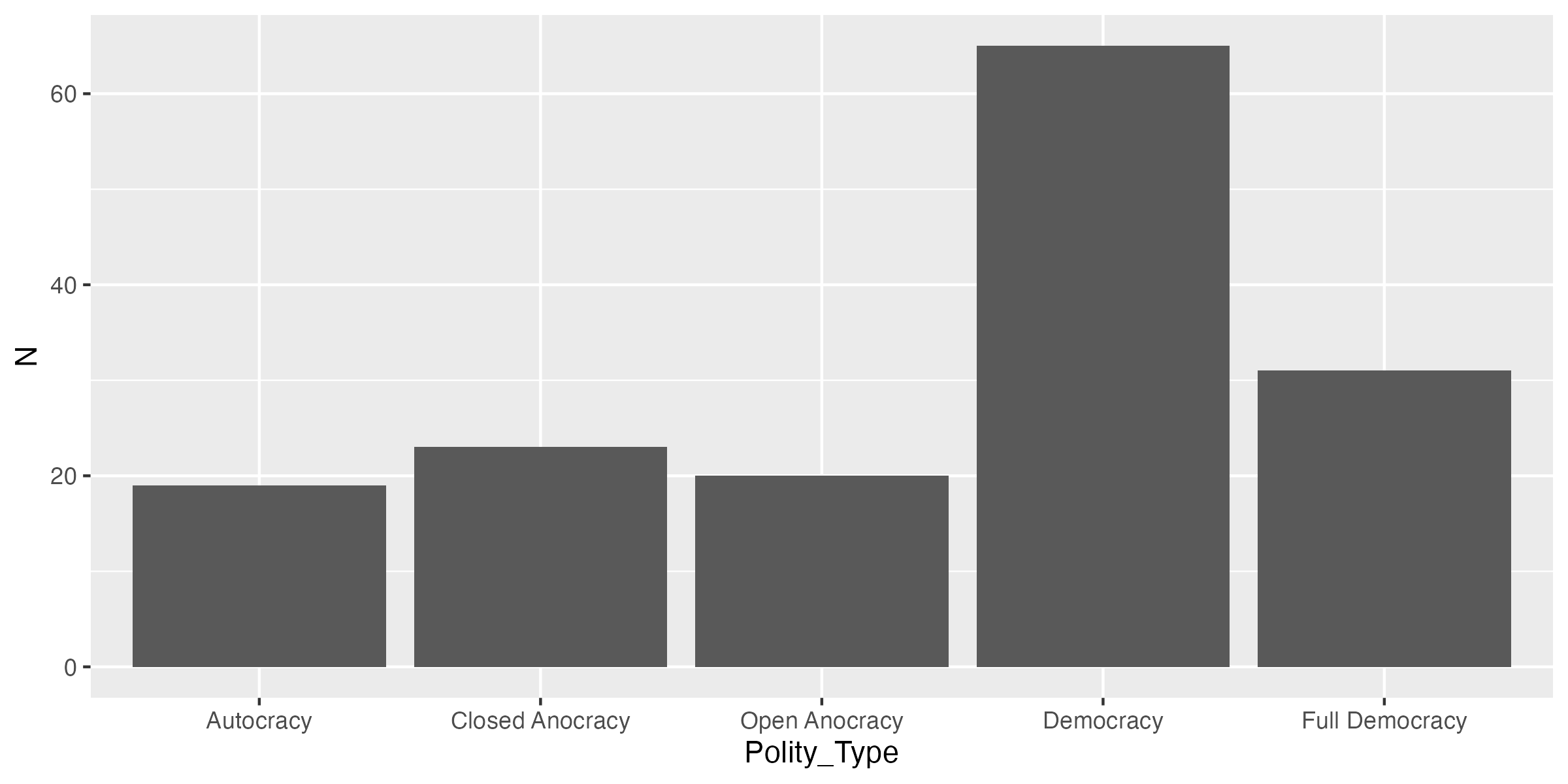
　まず、各政治体制（Polity_Type）に属する国家数の棒グラフを作ってみよう。作図に必要なdata.frameをdf3として用意しておく。

Code 10

df3 <- df |>
   drop_na(Polity_Type) |>
   mutate(Polity_Type = factor(Polity_Type,
                               levels = c("Autocracy", "Closed Anocracy",
                                          "Open Anocracy", "Democracy",
                                          "Full Democracy"))) |>
   group_by(Polity_Type) |>
   summarise(N = n())

df3

# A tibble: 5 × 2
  Polity_Type         N
  <fct>           <int>
1 Autocracy          19
2 Closed Anocracy    23
3 Open Anocracy      20
4 Democracy          65
5 Full Democracy     31

　棒グラフの作り方はこれまでのやり方と同じである。

Code 11

df3 |>
   ggplot() +
   geom_col(aes(x = Polity_Type, y = N))

　この棒グラフが持つ情報は2つである。まず、xで指定した政治体制のタイプ (Polity_Type)、そしてyで指定した国家数 (N)だ。ここに更にもう一つの次元を使いすると使用。たとえば、もう一つの次元として大陸（Continent）を使いするとしよう。この場合、作図に使用するデータには大陸の変数（列）も必要だ。一方、先ほど作成したdf3には大陸の情報がない。まずは、政治体制\(\times\)大陸ごとの国家数を計算し、df4として格納しておく。

Code 12

df4 <- df |>
   drop_na(Polity_Type) |>
   mutate(Polity_Type = factor(Polity_Type,
                               levels = c("Autocracy", "Closed Anocracy",
                                          "Open Anocracy", "Democracy",
                                          "Full Democracy"))) |>
   group_by(Polity_Type, Continent) |>
   summarise(N       = n(),
             .groups = "drop")

df4

# A tibble: 20 × 3
   Polity_Type     Continent     N
   <fct>           <chr>     <int>
 1 Autocracy       Africa        3
 2 Autocracy       Asia         14
 3 Autocracy       Europe        2
 4 Closed Anocracy Africa       14
 5 Closed Anocracy America       2
 6 Closed Anocracy Asia          6
 7 Closed Anocracy Europe        1
 8 Open Anocracy   Africa       12
 9 Open Anocracy   America       4
10 Open Anocracy   Europe        2
11 Open Anocracy   Oceania       2
12 Democracy       Africa       18
13 Democracy       America      16
14 Democracy       Asia         15
15 Democracy       Europe       16
16 Full Democracy  Africa        1
17 Full Democracy  America       5
18 Full Democracy  Asia          3
19 Full Democracy  Europe       20
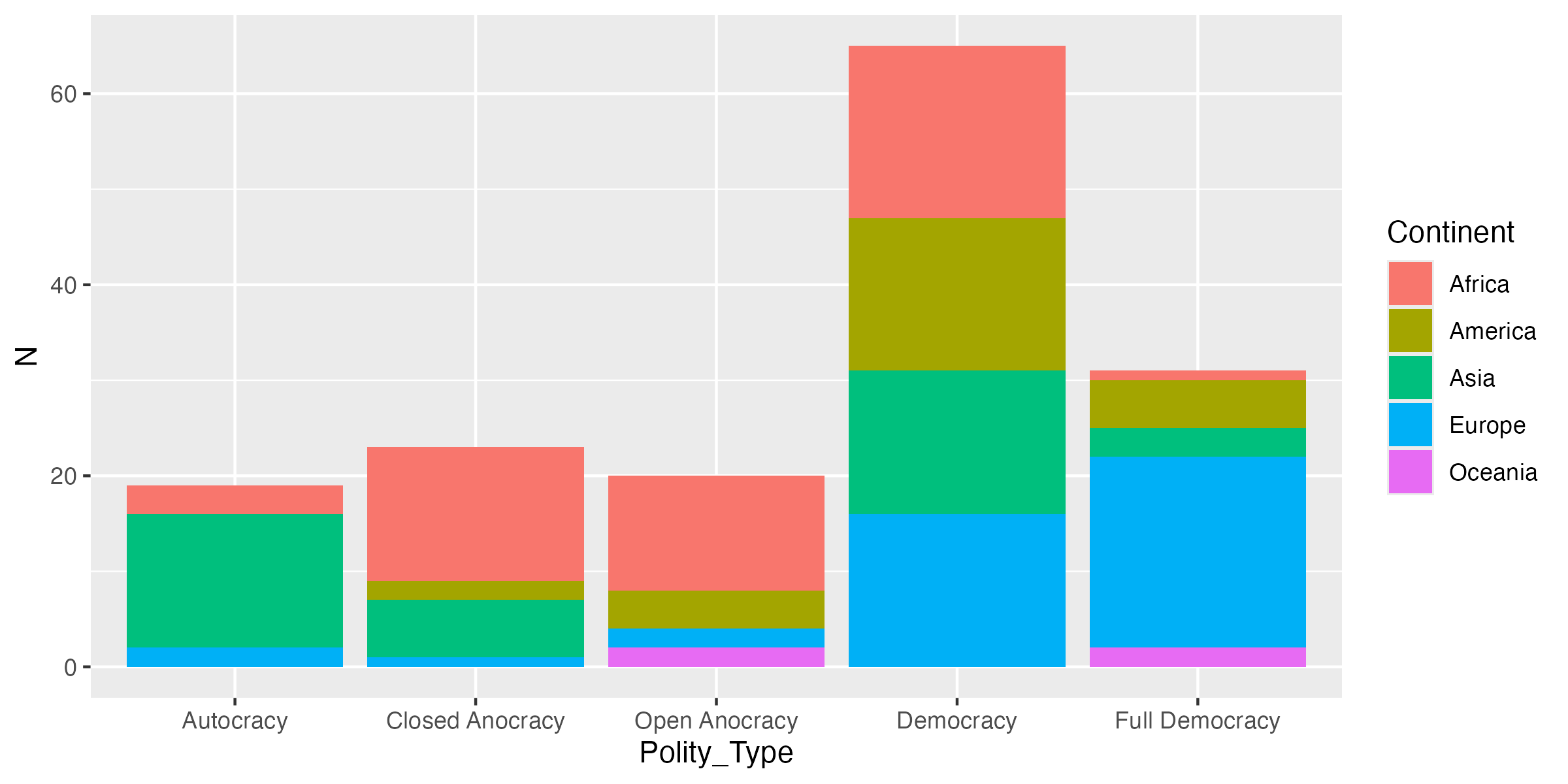
20 Full Democracy  Oceania       2

　次元を追加するときにはaes()内に引数を追加すれば良い。棒グラフの棒に更に情報を持たせるのであれば、どうすれば良いだろうか。棒は点・線・面のうち、面に該当する。面であるならば、面の色（fill）、枠線の色（color）、枠線のタイプ（linetype）、透明度（alpha）などがある。xとyのみと構成された多くの図において、もう一つの次元を追加するのであれば、定番は色である。棒グラフの場合、面の色と枠線の色をそれぞれ指定することができるが、ここでは面の色（fill）にマッピングする。やり方はaes()内にfill = Continentを追加するだけだ。

Code 13

df4 |>
  ggplot() +
  geom_col(aes(x = Polity_Type, y = N, fill = Continent))

　このような図を想像した人もいれば、少し違うと思う人もいるだろう。沖積されている形の棒グラフは世の中でそこそこ見るものであるが、実は分かりにくい図でもある。たとえば、民主主義（Democracy）の国の中で最も国家数が多い大陸はどこだろうか。この図ではどの大陸もだいたい同じ国家数にも見える。したがって、色分けした棒グラフは通所湯、棒の位置をずらす必要がある。ずらす方法はgeom_col()内にposition = "dodge"を指定するだけだ。注意する点はaes()の中でなく、外に指定することだ。

Code 14

df4 |>
  ggplot() +
  geom_col(aes(x = Polity_Type, y = N, fill = Continent),
           position = "dodge")

　あとは図を少しずつ調整してだけであるが、ここでは凡例の位置を変更する方法について紹介する。グラフ全体の見た目などを細かく調整するレイヤーはtheme()である。このtheme()内にlegend.position = "bottom"を指定すると、凡例が図の下段へ移動する。デフォルトは"right"であり、 　"top"は上段、"none"は削除を意味する。"left"も可能だが、あまり使われない。このtheme()はかなり奥深く、コンソール上で?themeを入力してみれば分かるだろうが、引数の数も数十種類以上だ。これをすべて覚えて使う人は少数だろう。多分、これは{ggplot2}の開発者にとっても同じはずである。必要に応じてヘルプやインターネット検索を活用すれば良い。

Code 15

df4 |>
  ggplot() +
  geom_col(aes(x = Polity_Type, y = N, fill = Continent),
           position = "dodge") +
  theme(legend.position = "bottom")

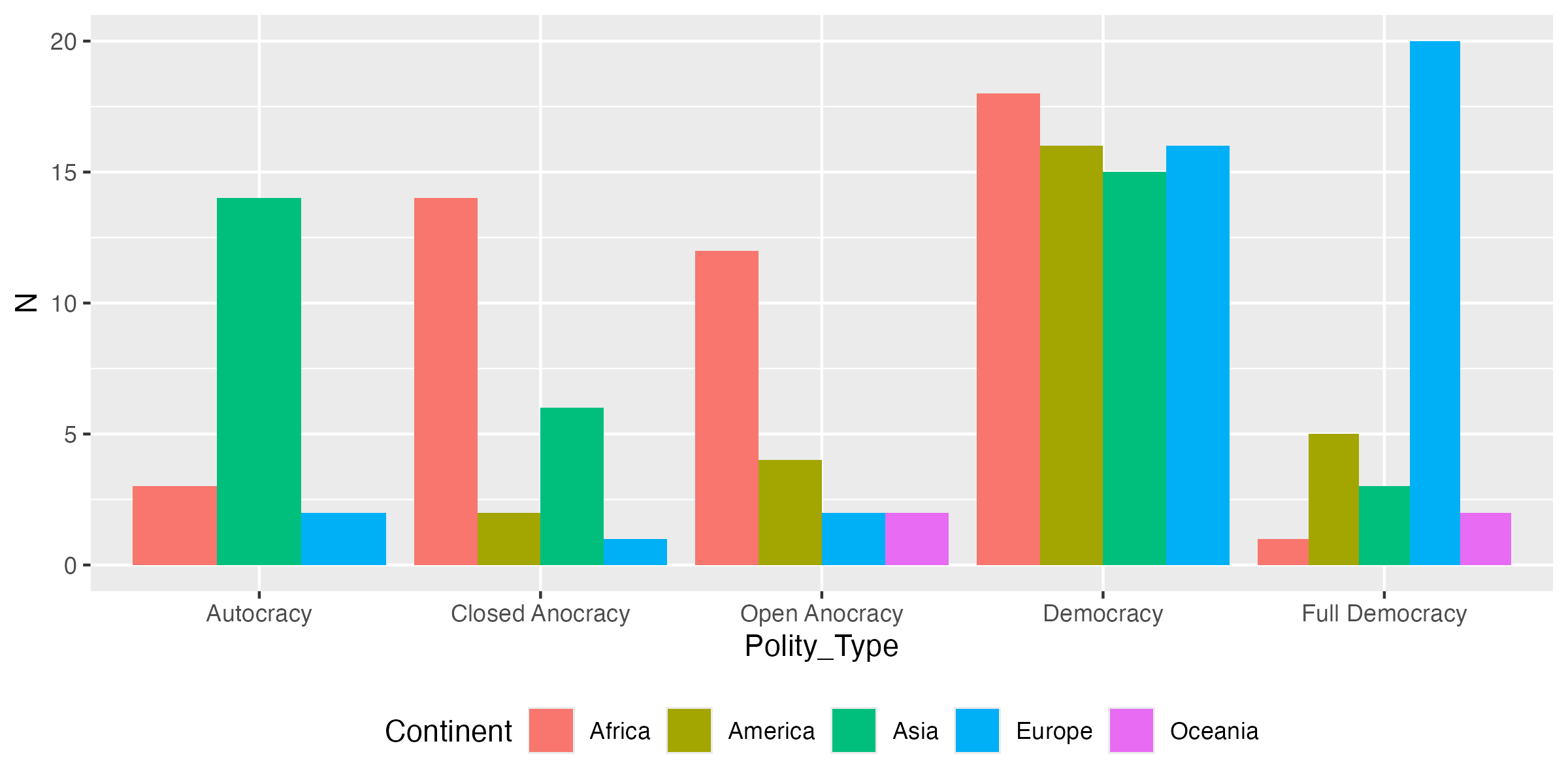
　続いて、全く同じ情報を持つグラフでありながら、だいぶ印象が変わるものを紹介しよう。これまで作成した棒グラフは「ある政治体制内の大陸の分布」を知ることに特化している。つまり、「権威主義国家内にはアフリカがXカ国、アジアが…」といったメッセージを伝えるに効果的である。一方、「ある大陸内の政治体制の分布」を見るにはどうすれば良いだろうか。つまり、「アフリカには権威主義がXカ国、民主主義が…」のメッセージを伝えることである。いずれも必要な変数は同じはずである。異なるのはマッピングだけである。たとえば、xとfillを交換してみよう。厳密に言えば棒を並び替えただけなのに、かなり印象が変わってくる。可視化は「伝えたいメッセージを効果的に伝える」ことが重要であり、そのためには試行錯誤が必要だろう。

Code 16

df4 |>
  ggplot() +
  geom_col(aes(x = Continent, y = N, fill = Polity_Type),
           position = "dodge", color = "white") +
  theme_bw() +
  labs(x = "Continent", y = "Number of Countries", fill = "Polity Type") +
  theme(legend.position = "bottom")

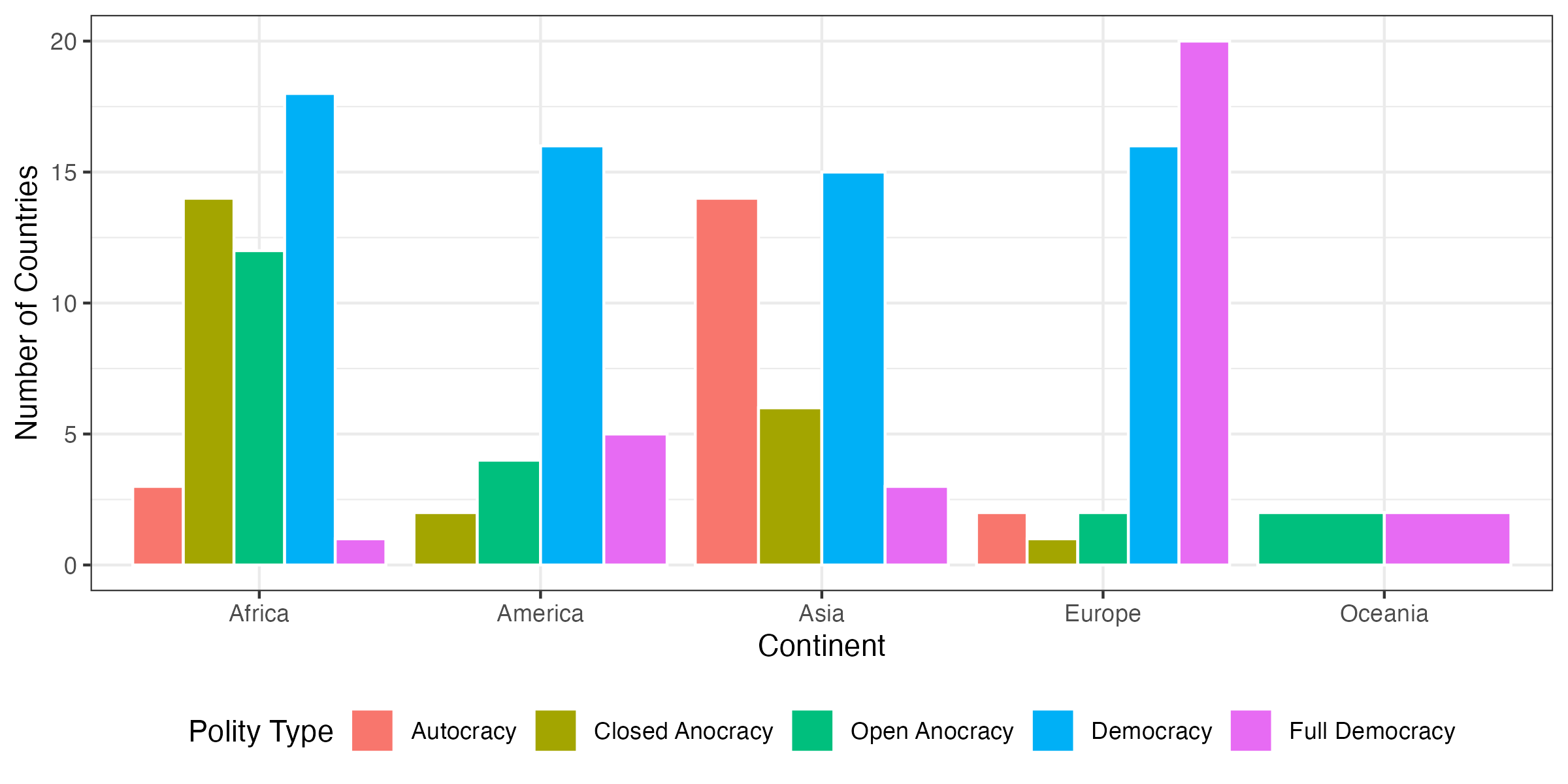
　最後に次元を追加するもう一つの方法として、ファセット（facet）分割について紹介する。これは色分けを出来る限り抑えたい時に効果的である。特に白黒印刷の場合、識別可能な色は白・グレー・黒の3つくらいだろう。しかし、色の種類は増えると、白黒印刷では識別するのが難しくなる。この場合、プロットの面（=ファセット）を分割することで色の増加が抑制できる。使い方はfacet_wrap(~ 分割の基準となる変数名)のレイヤーを入れるだけだ。df4を使い、政治体制ごとの国家数の棒グラフを作成する。ただし、それぞれの棒グラフは大陸ごとに独立したファセットを持つとする。

Code 17

bar_plot2 <- df4 |>
  ggplot() +
  geom_col(aes(x = Polity_Type, y = N)) +
  facet_wrap(~ Continent, ncol = 5) # ncol/nrowで列/行数の指定が可能

bar_plot2

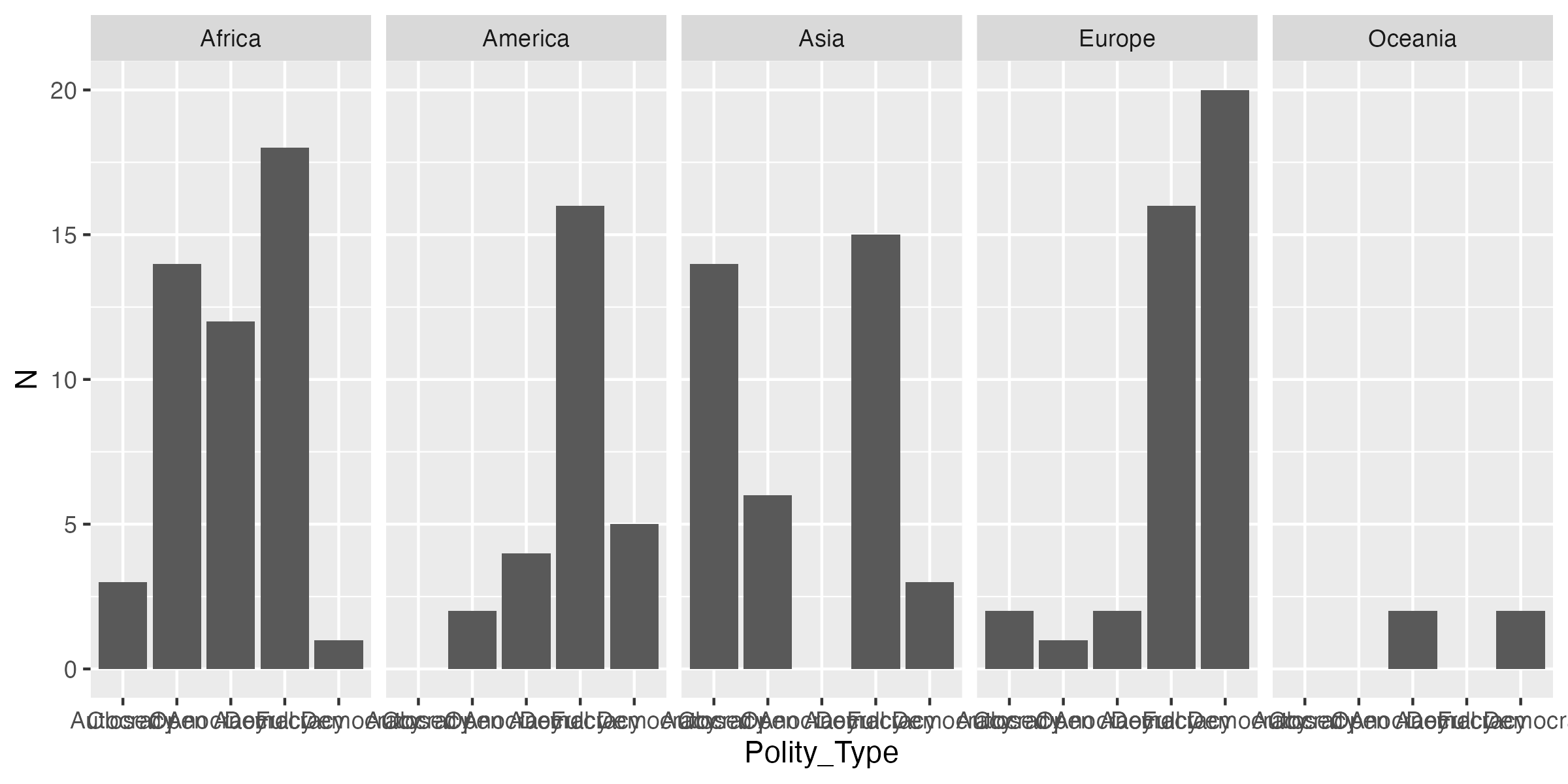
　ただし、このbar_plot2は値のラベルが重なっており、非常に読みにくい。この場合、ラベルを回転すると読みやすくなるだろう。横軸の目盛りラベルを修正するためにはtheme()レイヤーを追加し、axis.text.xを指定する必要がある。しかし、theme()レイヤーの中身はかなり複雑であるため、これを覚える必要はない。必要に応じてググれば良いだろう。今後、ラベルの回転が必要な場合は以下のコードからangleだけを修正すれば良い。以下の例は35度回転の例である。

Code 18

bar_plot3 <- bar_plot2 +
   labs(x = "Number of Countries", y = "Poltiy Type") + # ラベル修正
   theme_minimal() + # テーマを変えてみよう
   theme(axis.text.x        = element_text(angle = 35, vjust = 1, hjust = 1), # 35度回転
         panel.grid.major.x = element_blank()) # 横軸のグリッドを削除するおまじない

bar_plot3

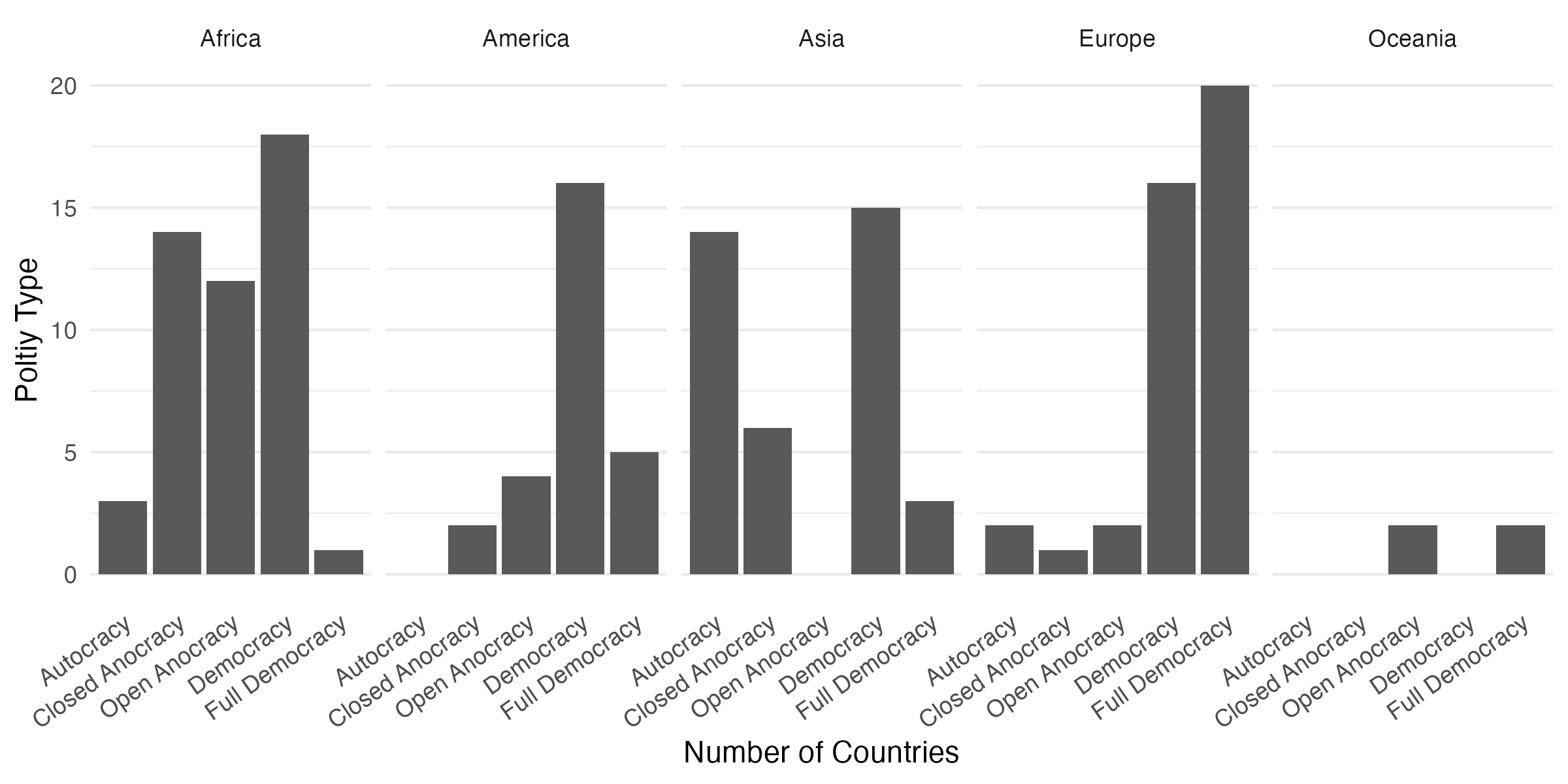
　もう一つの方法としてマッピング交換が考えられる。今の横軸を縦軸にすれば、長い文字列でも問題なく出力できるだろう。

Code 19

bar_plot4 <- df4 |>
  ggplot() +
  geom_col(aes(x = N, y = Polity_Type)) +
  labs(x = "Number of Countries", y = "Poltiy Type") +
  facet_wrap(~ Continent, ncol = 5) + # 5列のファセット分割
  theme_minimal(base_size = 12) +     # フォントサイズの調整も可能
  theme(panel.grid.major.y = element_blank()) # 縦軸のグリッドを削除するおまじない
   
bar_plot4

図の保存

　作成した図をファイルとして保存する時には、まずベクトルとビットマップ、どのフォーマットで保存するかを考える必要がある。ベクトル画像（ 図 2 (a) ）の拡張子は.pdf（推奨）、.svgなどがあり、これらのファイルは図をいくら拡大しても図が綺麗なままだという利点がある。また、複雑な図（例えば、点が数百万個ある散布図など）でないなら、ファイルサイズも比較的小さい。ビットマップ画像（ 図 2 (b) ）の拡張子は.png（推奨）、.bmp、.jpg（= .jpeg）などがあり、図がいくら複雑でもファイルサイズが安定するといったメリットがある。しかし、拡大すると図がカクカクする場合がある。高い解像度（DPI）にすると、拡大しても綺麗だが、ファイルサイズに注意する必要がある。基本的にベクトル画像を推奨するが、使用するワードソフトによってはPDFの図の埋め込みができない場合もある。ビートマップ画像はどのソフトでも確実に埋め込める。

(a) ベクトル画像

 

(b) ビットマップ画像

図 2: ベクトル画像とビットマップ画像

　ここではbar_plot3を高解像度の.png形式で保存する方法について解説する。{ggplot2}で作図した図の保存にはggsave()関数が便利だ。たとえば、作業フォルダー内のFigsフォルダにFigure1.pngという名でbar_plot3を保存するとしよう。ただし、予め作業フォルダー内にFigsフォルダーを作成しておく必要がある。図のサイズは幅6インチ、高さ3インチとし、解像度（DPI）は400とする。解像度が高いほどファイルサイズは大きくなるため、適切な解像度を選ぶのが重要だ。モニター画面に表示するだけなら最低150、印刷目的なら最低300はほしい。また、図の保存時、文字化けを防いでくれる{ragg}パッケージがあるが、これも予めインストールしておこう（JDCat分析ツールでは導入済み）。ggsave()の使い方の例は以下の通りである。

Code 20

ggsave(filename = "Figs/Figure1.png", # 保存先とファイル名
       plot     = bar_plot3,          # 保存する図のオブジェクト名
       width    = 6,                  # 図の幅 (インチ)
       height   = 3,                  # 図の高さ (インチ)
       dpi      = 400,                # 解像度
       device   = ragg::agg_png)      # 文字化け防止

ヒストグラム

変数の分布

　ヒストグラムは連続変数（=間隔尺度と比率尺度）の分布を確認する普遍的な可視化方法です。実習用データの例だと、大陸（Continent）列は離散変数（=名目尺度と順序尺度）であり、名目変数の分布は「アジアはXXカ国、アフリカはXXカ国、…」といった形で示され、これまで見てきた棒グラフで可視化する事ができる。一方、変数が連続変数の場合はヒストグラムと箱ひげ図が頻繁に使われる。

　以上の例はあくまでも一つの変数の分布を確認するものである。変数が2つになると、分布よりも2つの変数間の関係を確認することとなる。これは次回に紹介する散布図（連続変数\(\times\)連続変数）と折れ線グラフ（順序変数\(\times\)連続変数）で可視化することができる¹。

ヒストグラムの作成

　ヒストグラムの見た目は棒グラフと非常に似ている。棒グラフとヒストグラムの違いは棒と棒の間に隙間があるかないかである。棒グラフの場合は隙間がある。横軸が大陸の棒グラフの場合、アフリカとアジアの間の値というものは存在しない。なぜなら、名目尺度はそもそも数字でないか、数値であってもその数値の値に意味がないからだ。また、順序変数の場合、1位と2位の間の値は存在しない。つまり、1.5位といった順位は存在しない。一方、人間開発指数のような連続変数は0.1と0.2の間には無数の値が存在する。棒を並べるとしたら隙間なく棒を並べる必要があろう。

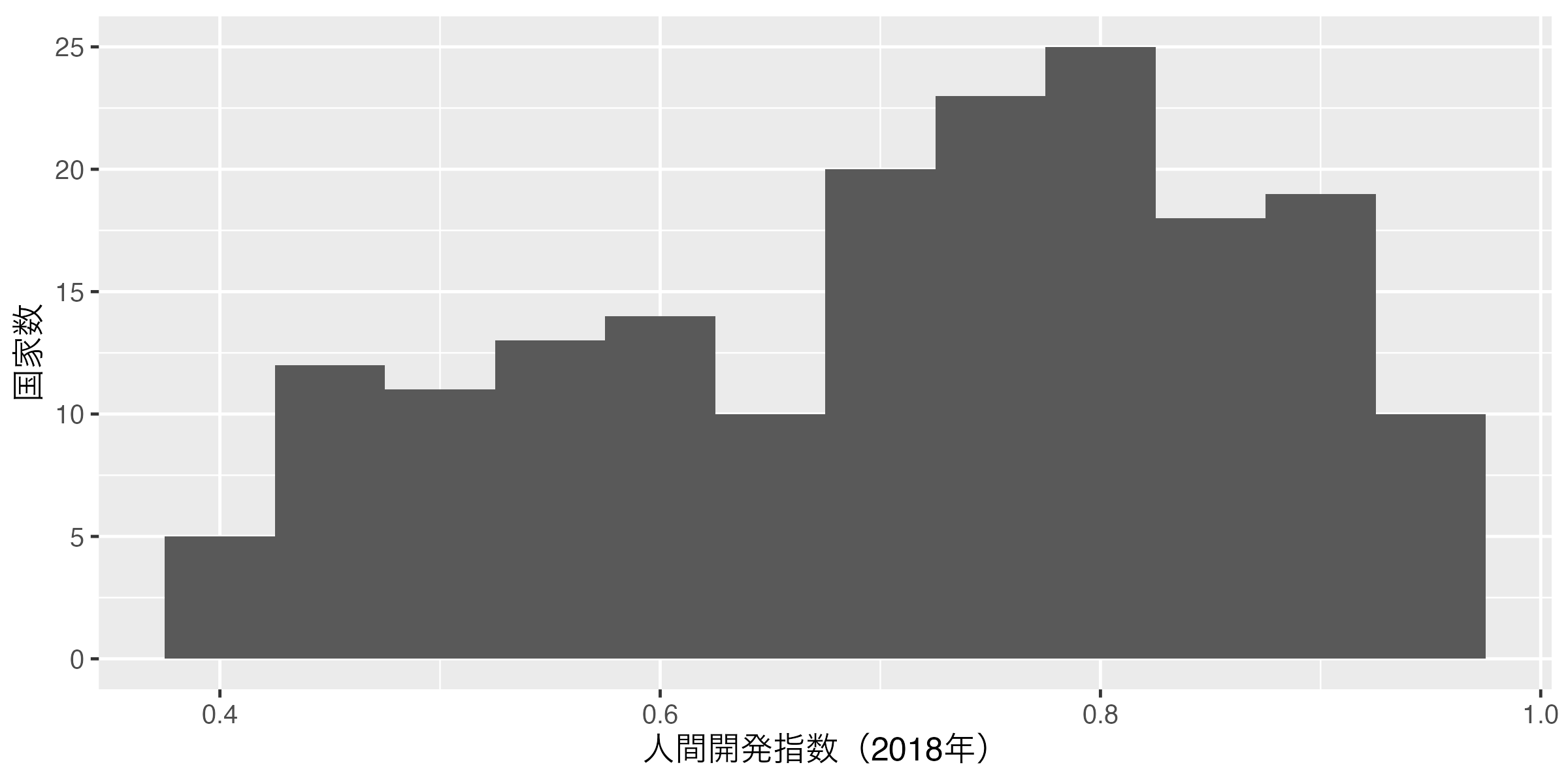
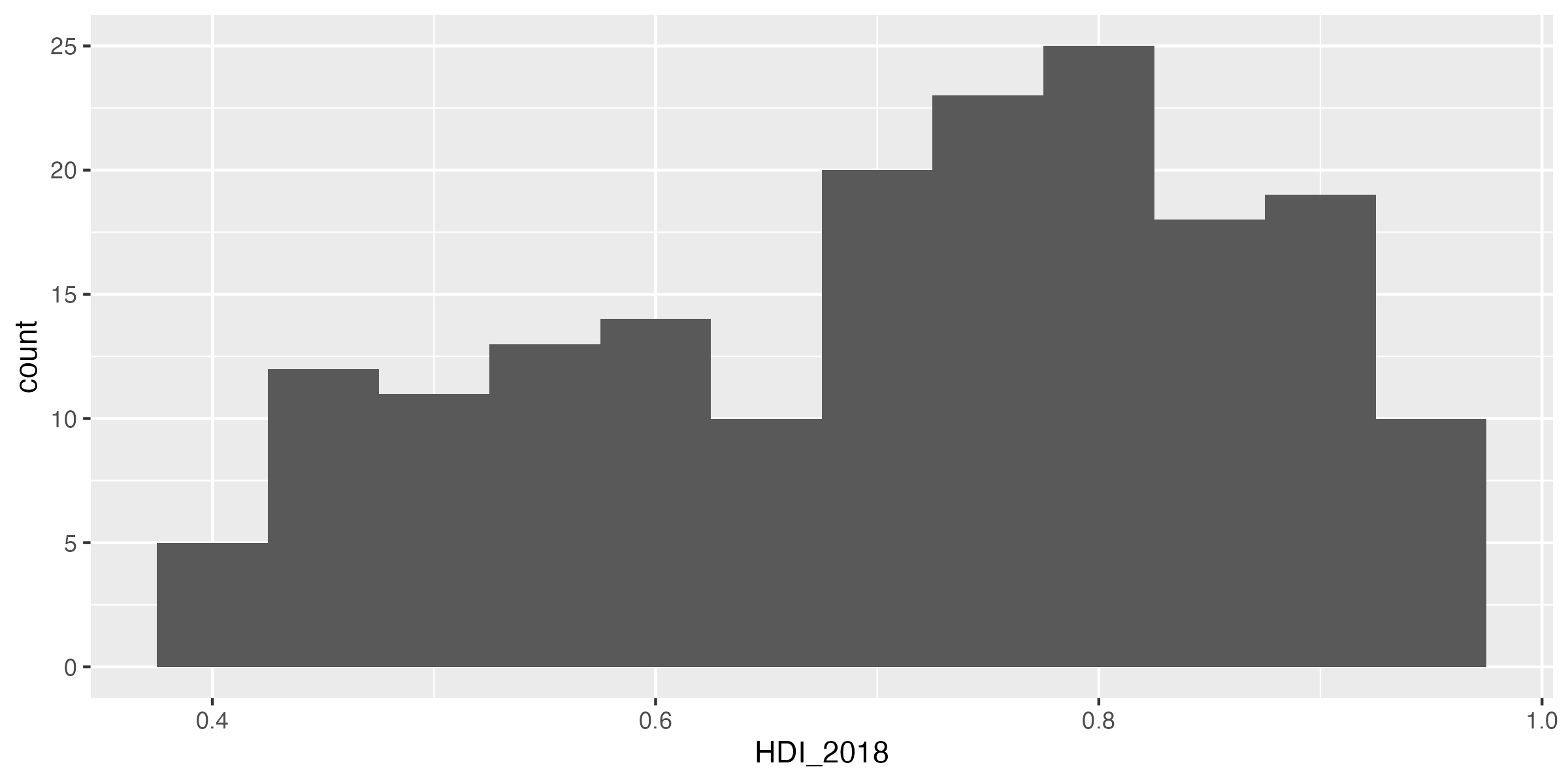
　それでも見た目は棒グラフと非常に似ているため、それぞれの棒には棒の横軸上の位置と高さという情報が含まれている。ただし、{ggplot2}を使ったヒストグラムの作成は非常に簡単である。{ggplot2}ではgeom_histogram()を使用するが、ヒストグラムを出力する変数をxにマッピングするだけで、棒の高さは自動的に計算される。つまり、yに対してマッピングを行う必要はなく、xのみで十分である。それではdf内の人間開発指数（HDI_2018）のヒストグラムを作成してみよう。

Code 21

df |>
  ggplot() +
  geom_histogram(aes(x = HDI_2018)) # HDI_2018のヒストグラム

　ヒストグラムは連続変数の分布を素早く確認することが目的である。たとえば、分布において峰がいくつか、峰がある場合、どの辺が最も度数/密度が高いかを素早く判断できれば良いヒストグラムと言えよう。棒の数を調整する。

　以下の3つのヒストグラムを比較してみよう。 図 3 (a) はヒストグラムが非常にギザギザしている。峰が10個くらいはありそうだ。一方、 図 3 (b) だと0.5と0.8周辺に大きな2つの峰があるように見える。最後に 図 3 (c) では0.8周辺に1つの峰が確認できる。

(a) 棒の幅が狭いヒストグラム

(b) 棒の幅が中程度のヒストグラム

(c) 棒の幅が広いヒストグラム

図 3: 3つのヒストグラム

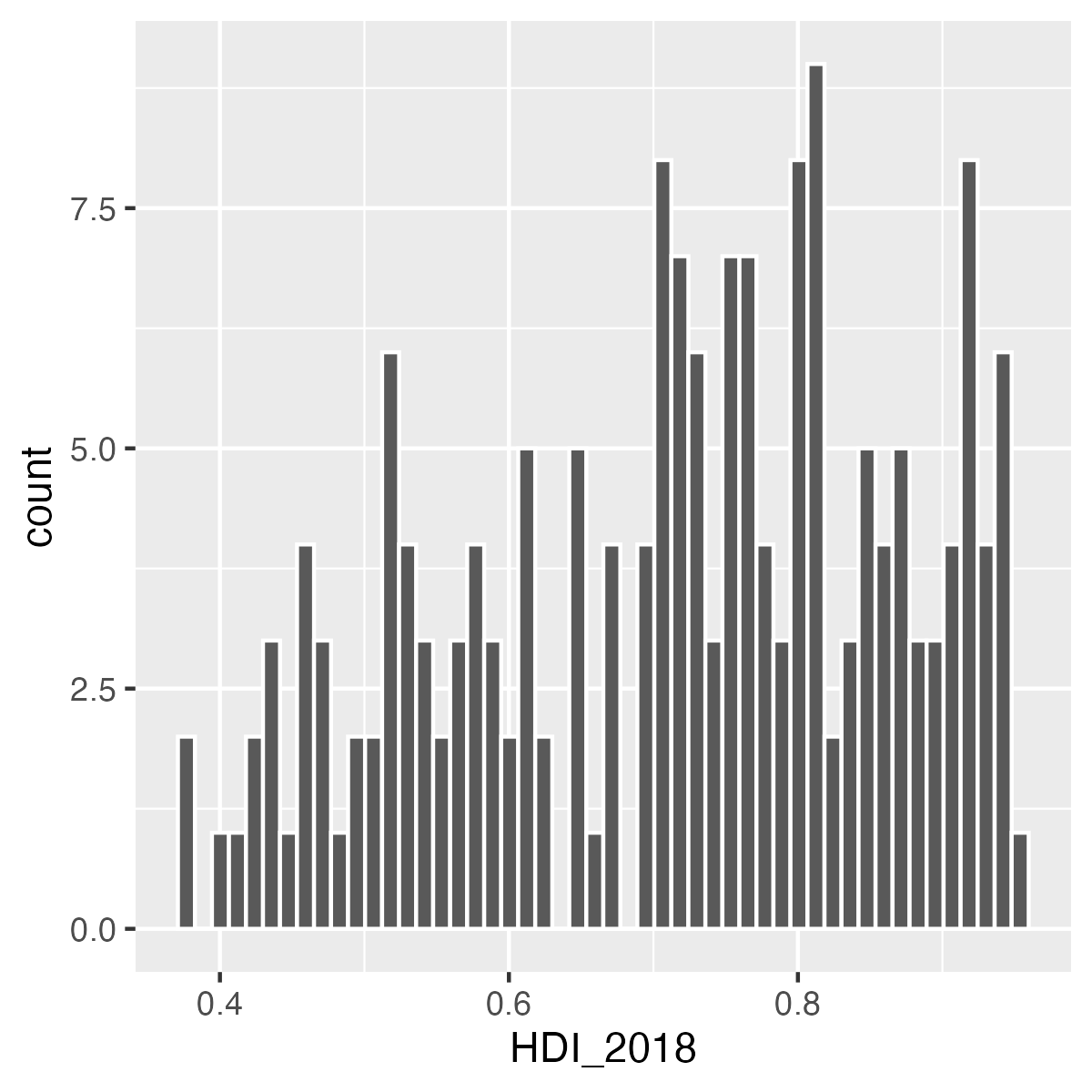
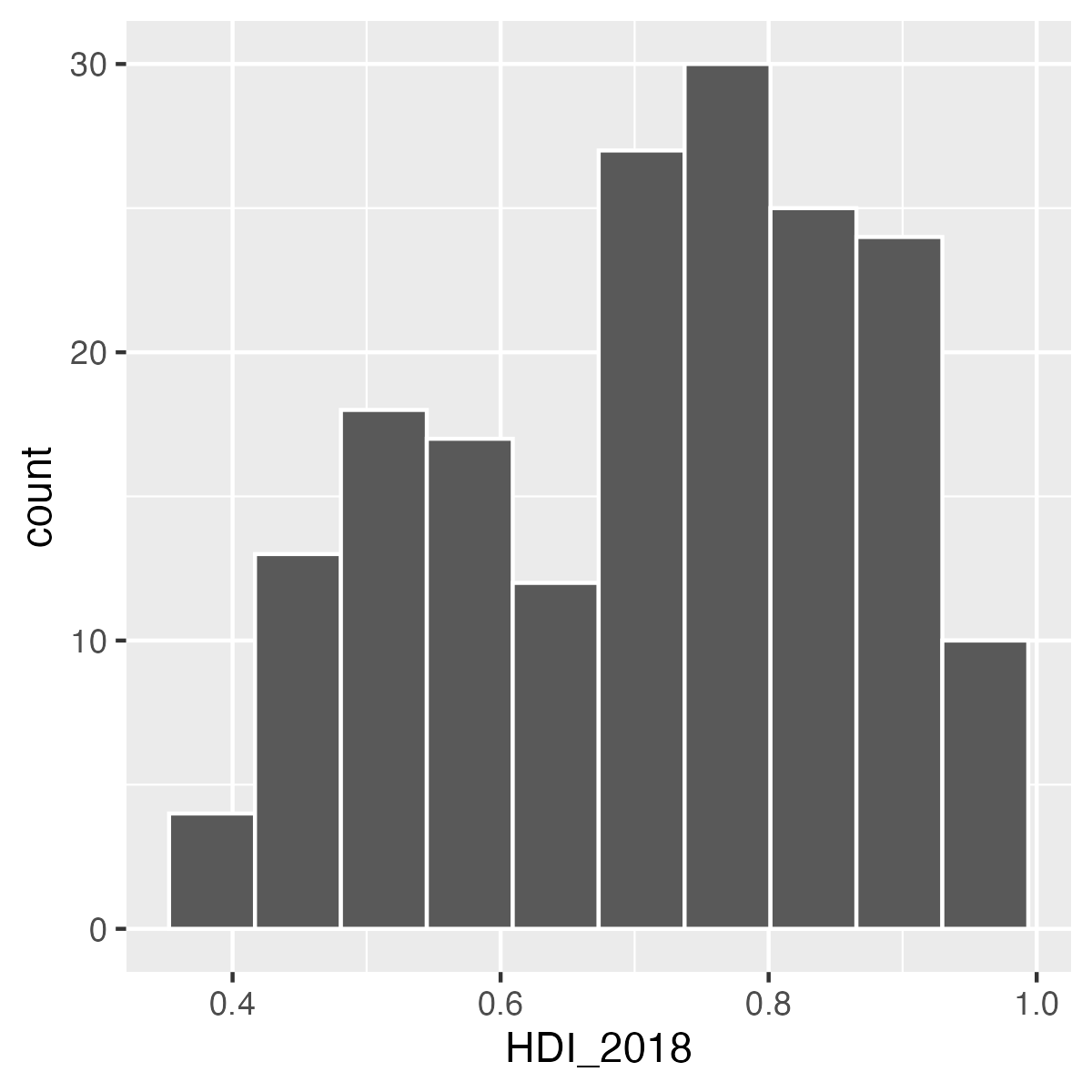
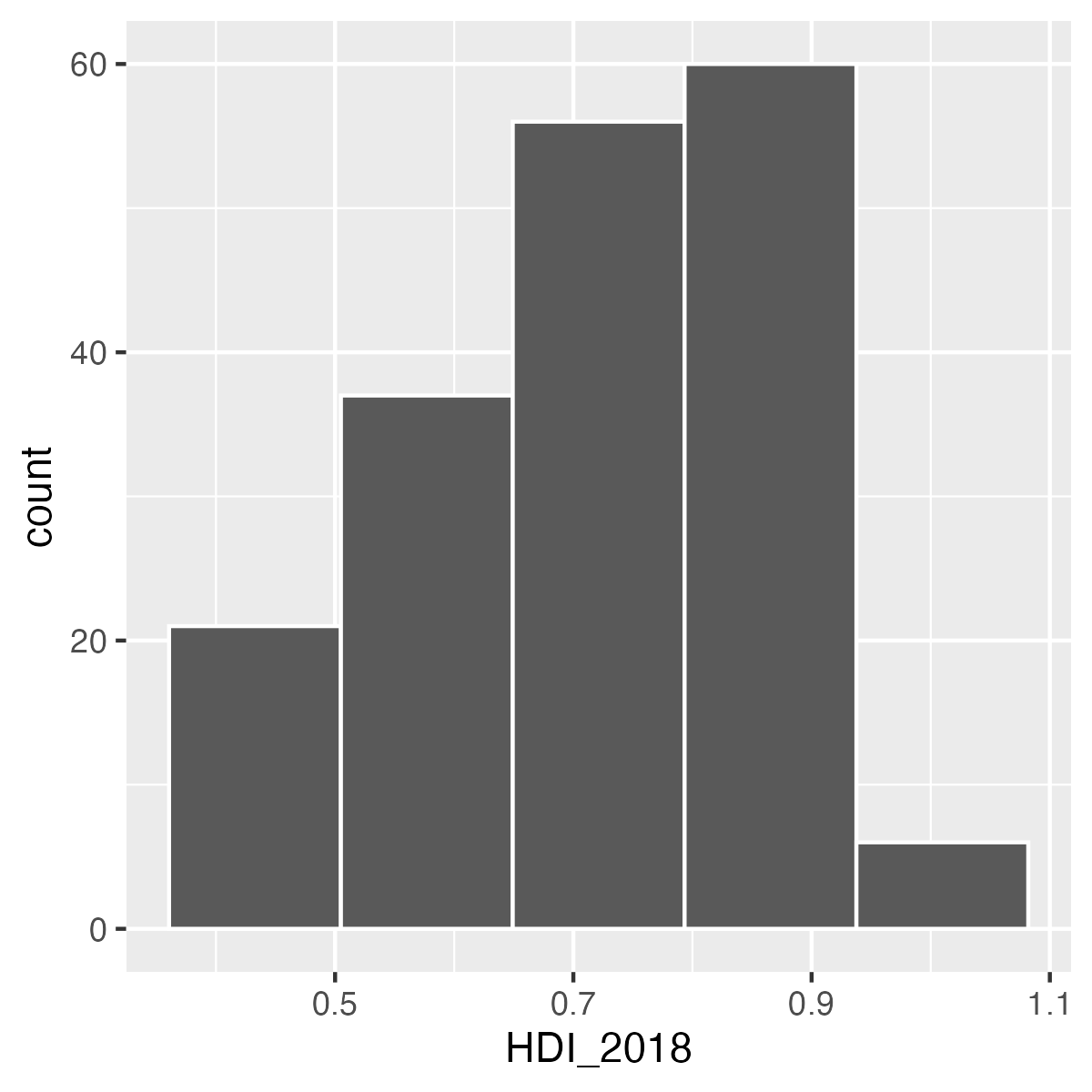
　この3つの図の中で、良い図はなんだろうか。まず、 図 3 (c) はあまりにも多くの情報が失われている。たとえば、0.5周辺の峰という情報がない。一方、 図 3 (b) は情報が多すぎる。その意味で 図 3 (b) が適切だろう。しかし、これは作図する側の人が決めるものであり、いくつかの図を出して比較してみるのが良いだろう。以上の3つの図は、ヒストグラムの棒の数を調整したものである。棒の数はgeom_histogram()内、aes()の外にbins引数を指定することで変更することができる。たとえば、 図 3 (b) は棒が10本のヒストグラムである²。これを再現するためにはbins = 10を指定すれば良い³。ちなみに、デフォルトはbins = 30となっている。

Code 22

df |>
  ggplot() +
  geom_histogram(aes(x = HDI_2018), bins = 10) # 棒を10本にする

　棒の本数が少ないことは、棒の幅が広いことを意味する。これは棒の数でなく、棒の幅から見た目を調整することもできることを意味し、geom_histogram()内、aes()の外にbinwidth引数を指定することで調整可能である。注意点としてはbinsとbinswidthは片方のみ指定可能で両方指定することは出来ないことだ。

Code 23

df |>
  ggplot() +
  geom_histogram(aes(x = HDI_2018), binwidth = 0.05) # 棒の幅を0.05にする

　ヒストグラムをより見やすくするコツとして、棒の枠線を追加することも考えられる。データ・インク比の観点から見ると枠線という視覚情報が追加されるので余計なものかも知れないが、枠線を入れるかどうかは作図する側が判断すれば良い。棒の枠線はgeom_histogram()内、aes()の外にcolor引数を指定可能であり、棒の面の色が黒に近いので枠線は白（"white"）に指定してみよう。

Code 24

hist_plot1 <- df |>
  ggplot() +
  geom_histogram(aes(x = HDI_2018), binwidth = 0.05, color = "white") +
  labs(x = "Human Development Index (2018)", y = "Number of Countries")

hist_plot1

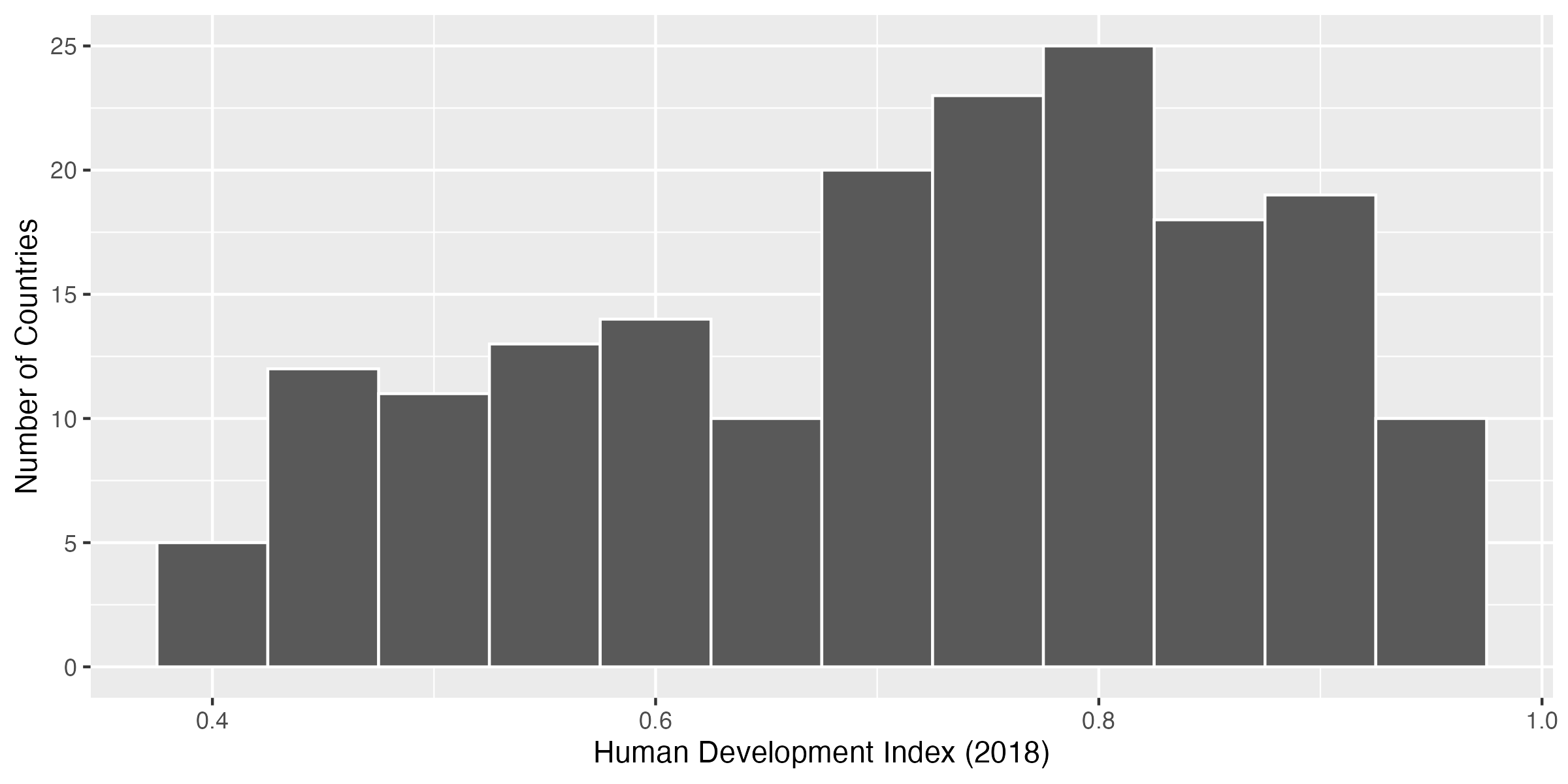
　最後に、横軸の目盛りを変更してみよう。今は目盛りが0.4、0.6、0.8、1.0の0.2kあん描くとなっている。この目盛りを調整するレイヤーはX軸の場合はscale_x_*()、Y軸の場合はscale_y_*()を使う。*の箇所には各軸の尺度を指定する。ヒストグラムは横軸も縦軸も連続した値であるので、scale_x_continuous()、scale_y_continuous()を使う。ここではX軸の目盛りを変更するのでscale_x_continuous()を使ってみよう。必要な引数は目盛りの位置を指定するbreaks引数、目盛りのラベルを意味するlabels引数だ。それぞれ長さ1以上のベクトルを指定すれば良いが、breaksとlabelsに使用する実引数（=ベクトル）の長さは同じ長さである必要がある。また、labelsにはcharacter型ベクトルを指定することもできる。

　先ほど作成したhist_plot1に目盛り変更のレイヤを追加してみよう。目盛りは0.4から1.0まで0.1間隔で付け、目盛りラベルもそれぞれ対応する値を指定する。公差0.1の等差数列ベクトルなのでseq()関数が便利だろう。目盛り調整済みのヒストグラムはhist_plot2として格納、出力してみよう。

Code 25

hist_plot2 <- hist_plot1 +
   scale_x_continuous(breaks = seq(0.4, 1.0, by = 0.1),
                      labels = seq(0.4, 1.0, by = 0.1))

hist_plot2

次元の追加

　ヒストグラムにもう一つの次元を追加する場合、棒グラフと同じ技が使える。つまり、面の色分け、またはファセット分割である。棒グラフと異なる点は色分けよりもファセット分割の方が圧倒的に推奨される点だ。

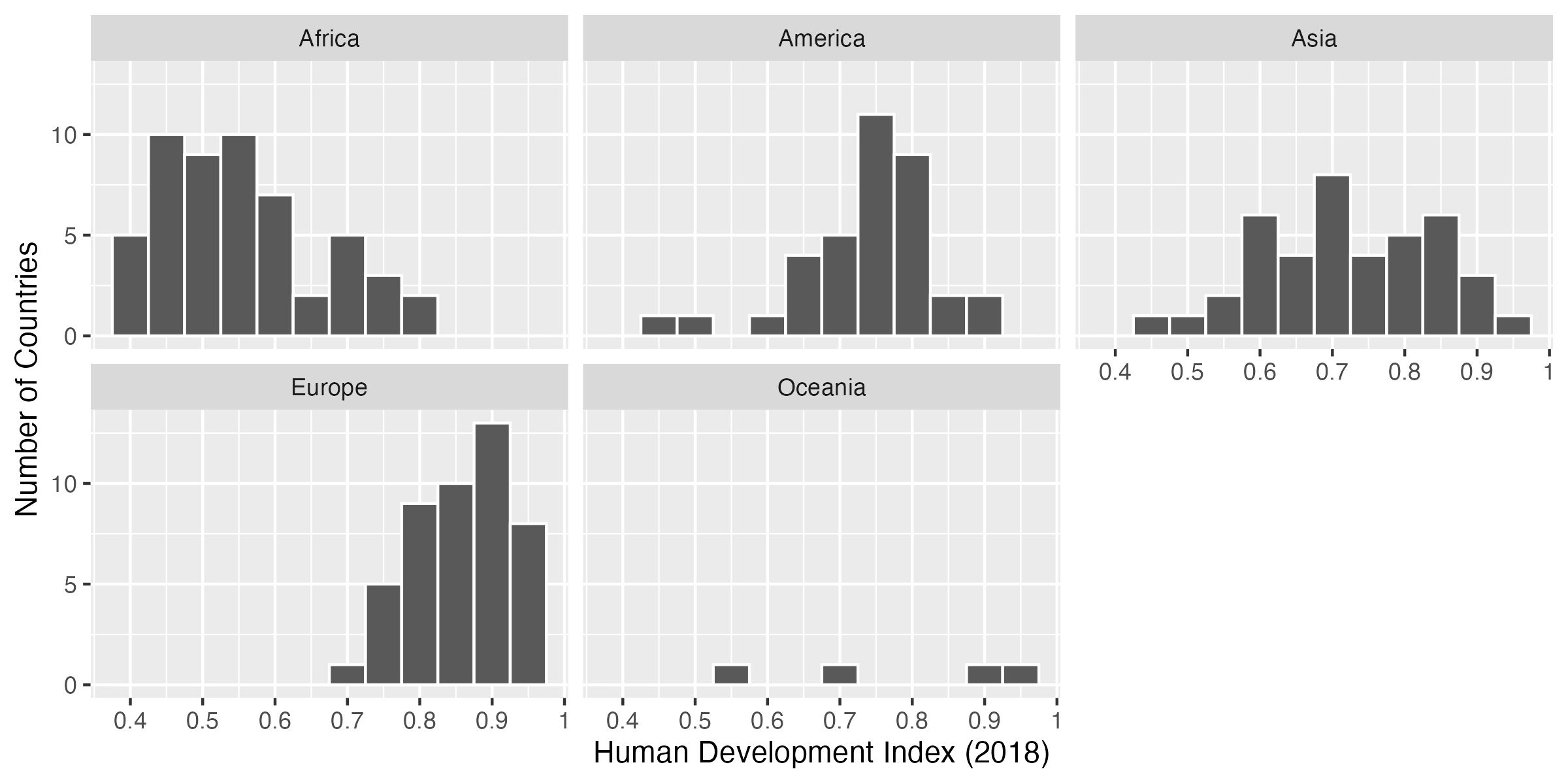
　まずはファセット分割から見よう。hist_plot2のヒストグラムは大陸（Continent）ごとに分ける場合、棒グラフと同様facet_wrap(~Continent)で分割できる。今回は2行3列で出力してみよう。facet_wrap()内にnrow = 2、またはncol = 3を追加するだけだ。

Code 26

hist_plot2 +
   facet_wrap(~Continent, nrow = 2)

　それでは色分けの例を見てみよう。棒グラフと同様、aes()内にfillを指定すれば良いが、注意すべき点としては棒グラフのようにposition = "identity"を追加する必要がある点だ。それではdfのOECDをリコーディング（1なら"OECD Members"、それ以外は"Others"）し、OECDの値ごとにヒストグラムの色分けをしてみよう。

Code 27

df |>
   mutate(OECD = if_else(OECD == 1, "OECD Members", "Others")) |>
   ggplot() +
   geom_histogram(aes(x = HDI_2018, fill = OECD), position = "identity",
                  binwidth = 0.05, color = "white") +
   labs(x = "Human Development Index (2018)", y = "Number of Countries",
        fill = "")

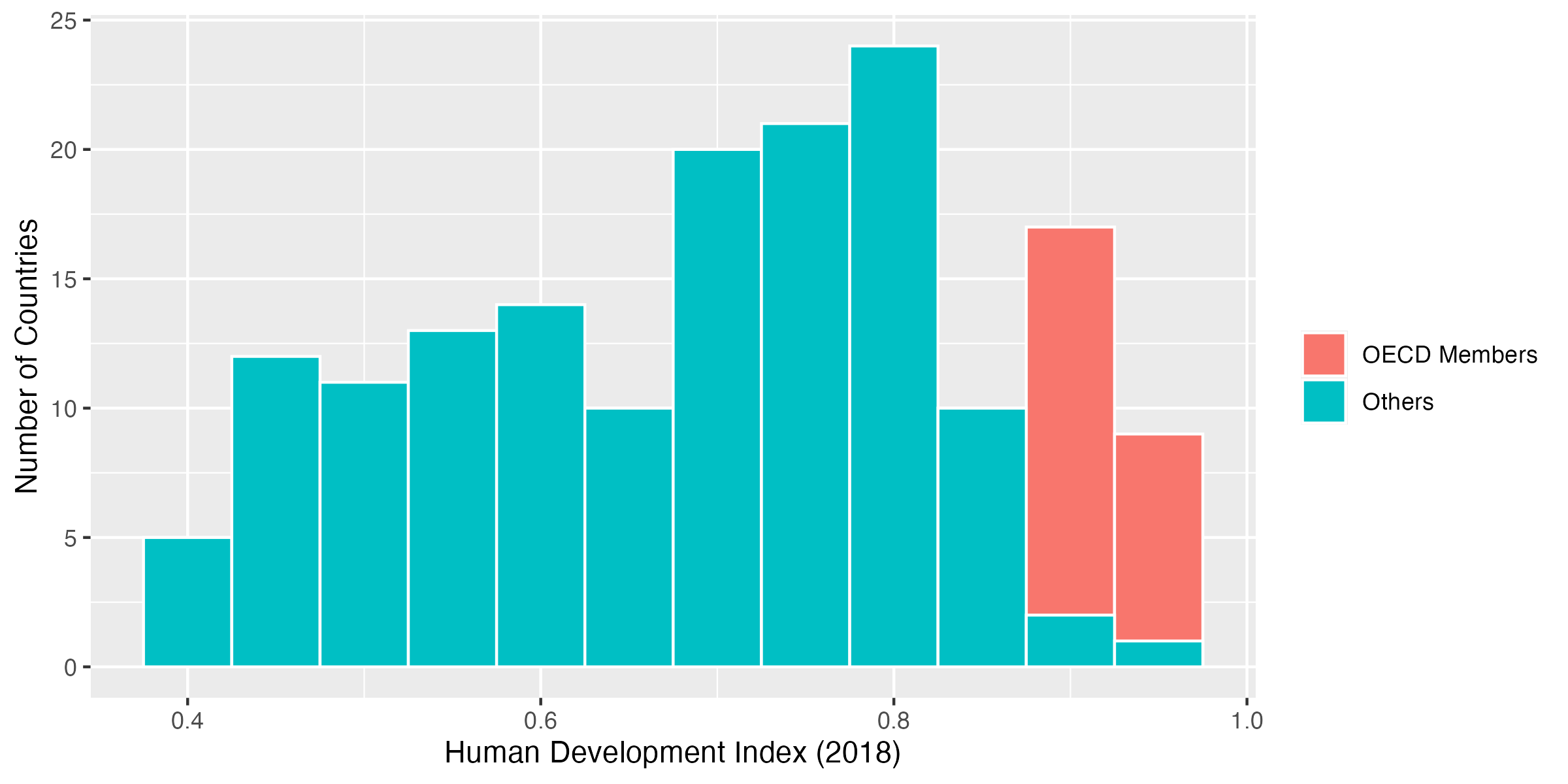
　このヒストグラムには深刻な問題がある。それはOECD加盟国の棒が非加盟国の棒の後ろに存在するため、一部の棒が消えているということだ。これを避けるためには棒をやや透明にする必要がある。透明度の調整はalphaで引数で行う。今回は全ての棒に対して適用するのでaes()の外側にalphaを指定する。alphaが1なら不透明、0なら透明となる。今回はalpha = 0.5程度に調整してみよう。

Code 28

df |>
   mutate(OECD = if_else(OECD == 1, "OECD Members", "Others")) |>
   ggplot() +
   geom_histogram(aes(x = HDI_2018, fill = OECD), position = "identity",
                  binwidth = 0.05, color = "white", alpha = 0.5) +
   labs(x = "Human Development Index (2018)", y = "Number of Countries",
        fill = "")

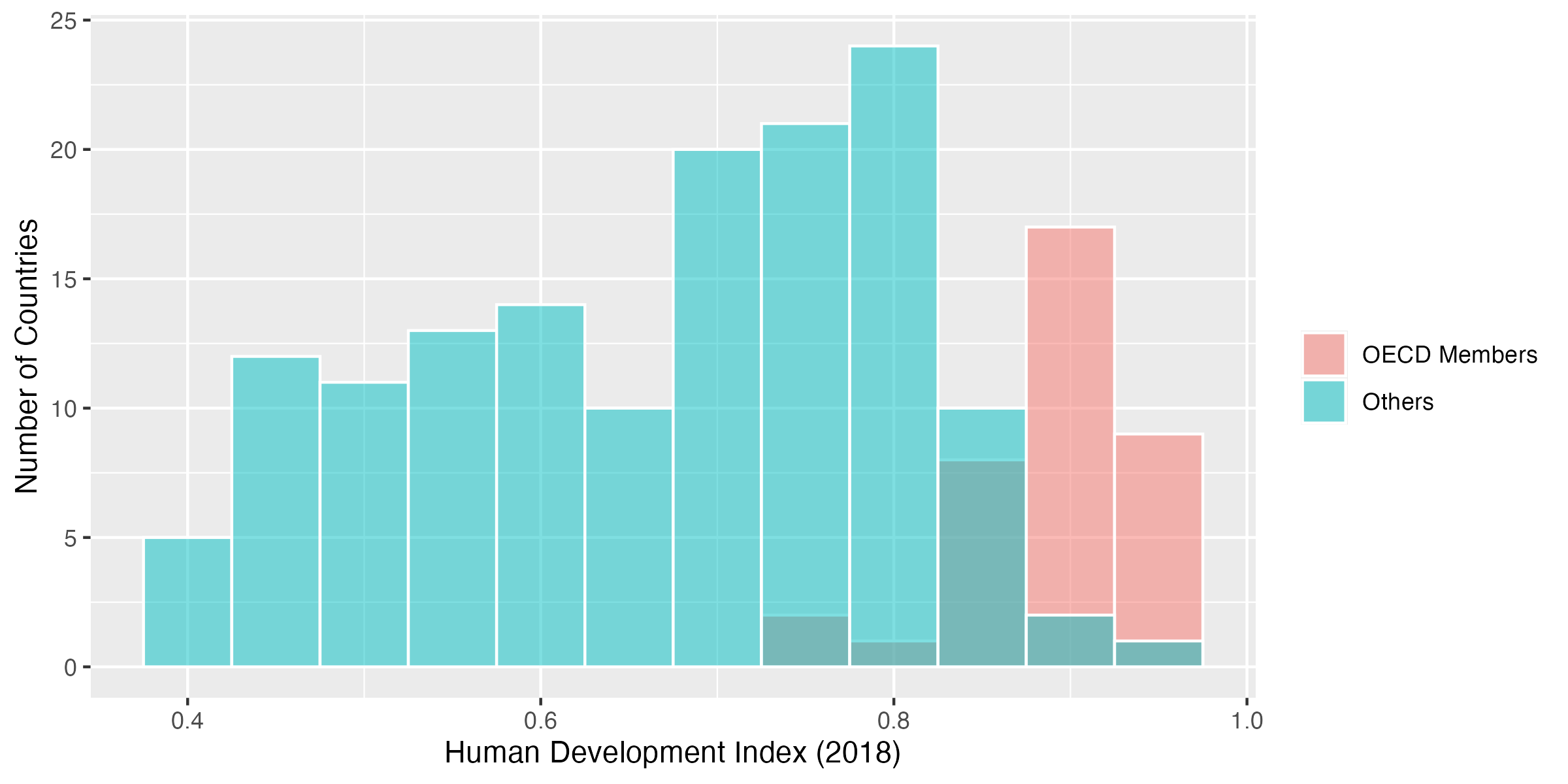
　このように非加盟国の棒の後ろに加盟国の棒が隠されていることが分かる。人によってはこのような色分けヒストグラムでも良いと思うかも知れない。しかし、色分けのヒストグラムはせいぜい2色までが限界である。もし、3色以上ならどうなるだろうか。たとえば、大陸（Continent）の値ごとに色分けをすればどうなるだろうか。

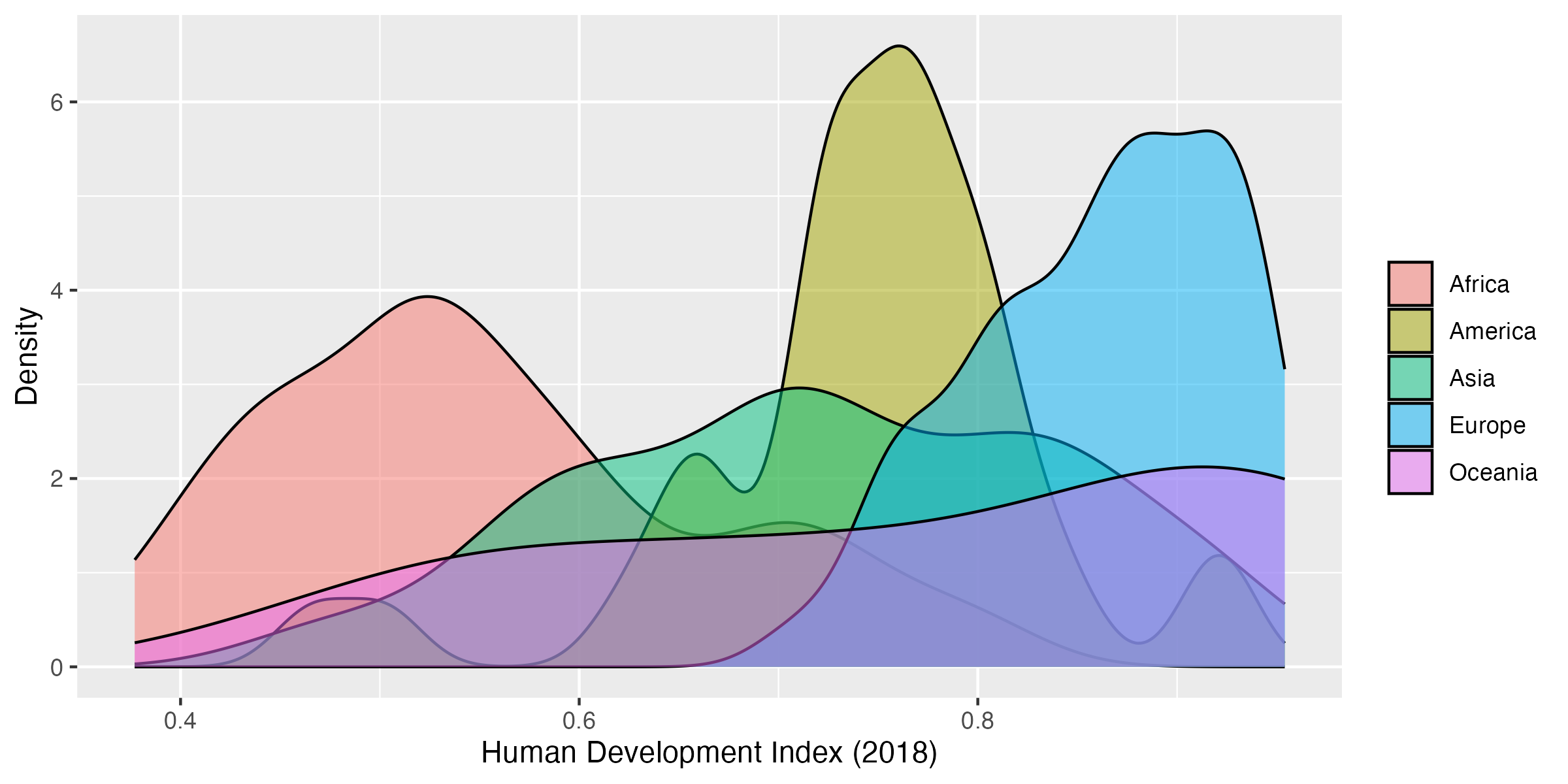
Code 29

df |>
   ggplot() +
   geom_histogram(aes(x = HDI_2018, fill = Continent), position = "identity",
                  binwidth = 0.05, color = "white", alpha = 0.5) +
   labs(x = "Human Development Index (2018)", y = "Number of Countries",
        fill = "")

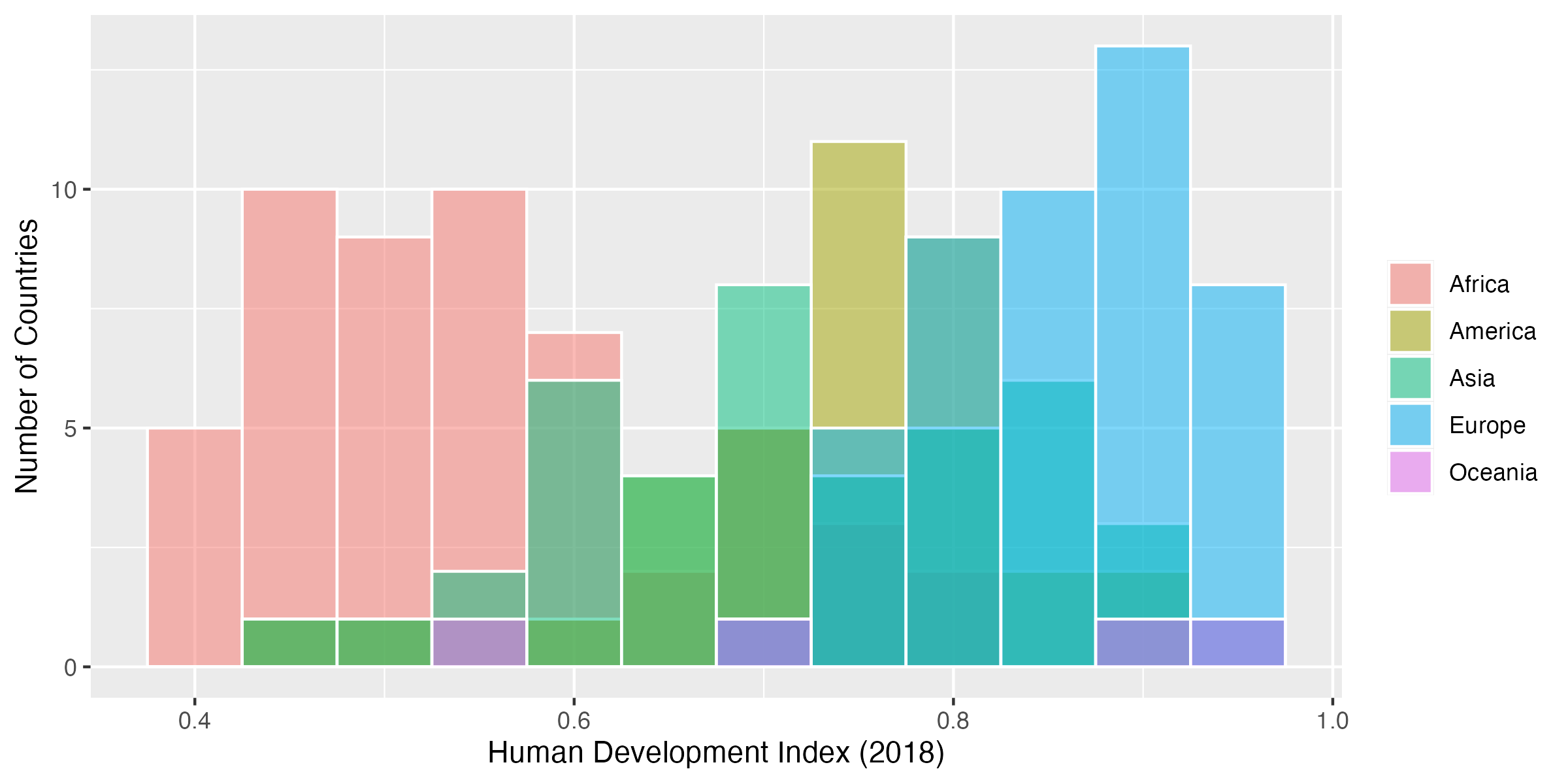
　我々はこのヒストグラムから一体どのような情報が読み取れるだろうか。

　ちなみに、position = "identity"がない場合、一つのヒストグラムのうち、各大陸が占める割合を見せることができる。ただし、これも読みづらい図であることには変わりない。

Code 30

df |>
   ggplot() +
   geom_histogram(aes(x = HDI_2018, fill = Continent), 
                  binwidth = 0.05, color = "white") +
   labs(x = "Human Development Index (2018)", y = "Number of Countries",
        fill = "")

　どうしても3つ以上のグループの分布を一つのファセットでオーバーラップしたい場合は、geom_histogram()の代わりにgeom_density()の使用を推奨する。これは密度曲線を出力する幾何オブジェクトであり、マッピングはヒストグラムと同じである。ただし、ヒストグラムではないためbinwidthやbins引数は不要であり、代わりにadjust引数を使う。デフォルトは1であるが、小さいほどギザギザの密度曲線が、大きいほど滑らかな密度曲線になる。また、縦軸が数（count）でなく、密度（density）になるため、解釈の際は注意が必要だ。

Code 31

df |>
   ggplot() +
   geom_density(aes(x = HDI_2018, fill = Continent), 
                alpha = 0.5, adjust = 0.8) +
   labs(x = "Human Development Index (2018)", y = "Density", fill = "")

教科書

• 『私たちのR: ベストプラクティスの探求』
  • 「可視化[基礎]」
  • 「可視化[応用]」

注

1. 他にも離散変数\(\times\)離散変数に使用するモザイク図がある。モザイク図については教科書の第20.16章を参照すること。また、名目尺度\(\times\)連続変数は棒グラフが有効である。大陸ごとの人間開発指数の平均値を示した棒グラフがその例である。

2. ちなみに、 図 3 (a) は50本、 図 3 (c) は5本である。

3. 厳密に言えば、棒が10本ではなく、区間が10個になることを意味する。分布を確認する変数を最小値と最大値までの範囲を10個の区間に分割し、それぞれの区間に属するケース数が表示される。したがって、特定の区間にケースがない場合は、棒の数は10本未満になる可能性がある。むろん、10本より多くなることはない。